sshateau (285pt, 11 solves)

Rev

Description:

Recently, I realized that the ark of the covenant is in a palace in the sky which is protected by 19 special angels! I am so curious to see the ark but I need to introduce myself as an insider with a watchword… Would you mind helping me enter this palace, please?

Palace address: 76.74.170.201:2020

Files:

• sshd

Overview:

We are given a sshd binary and a remote address to connect to. When we try to ssh at this address, sure enough we connect and are prompted for a password:

$ ssh 76.74.170.201 -p 2020
The authenticity of host '[76.74.170.201]:2020 ([76.74.170.201]:2020)' can't be established.
ECDSA key fingerprint is SHA256:UPVqys5AOxQwfeh6shfz8Stg93agzYYZedQS4j75UBw.
Are you sure you want to continue connecting (yes/no)? yes
Warning: Permanently added '[76.74.170.201]:2020' (ECDSA) to the list of known hosts.
[email protected]'s password:

From the challenge description it sounds like there is a backdoor hidden in this version of sshd and we need to find it.

Part 0: reference binary

The sshd binary is very large and was compiled without debugging symbols, in order to get our bearings it will be useful to try to compare it to a “clean” version of sshd so we can see what parts were modified. Additionally for the purposes of finding the patch, it will also be useful to have a reference sshd that was compiled with similar settings so the patch stands out.

In the usage printout, we see:

OpenSSH_8.3p1, OpenSSL 1.1.1  11 Sep 2018
usage: sshd [-46DdeiqTt] [-C connection_spec] [-c host_cert_file]
            [-E log_file] [-f config_file] [-g login_grace_time]
            [-h host_key_file] [-o option] [-p port] [-u len]

8.3p1 is the ssh version here and we can download a tarball of source from any of these mirrors: https://www.openssh.com/portable.html#downloads. Specifically we want openssh-8.3p1.tar.gz.

After unpacking the directory, we can compile two reference versions:

With debugging symbols:

./configure CFLAGS='-g'
make

Without debugging symbols (for hexdiff):

./configure
make

I’ve attached my two versions: with symbols and without symbols.

Part 1: finding a patch

The next step is to try to figure out what has been changed in the custom binary. I opened up the provided sshd and the reference compiled without symbols in Hex Fiend (a hex utility app) and compared them.

For the most part, the binaries were very similar and most of the changes were simply the LSB of an address. The reference binary was a bit bigger (likely compiled with extra features) and I found a few sections that were not present in the provided sshd.

Eventually I stumbled upon a large chunk of high entropy data that was found in the custom sshd and not the reference:

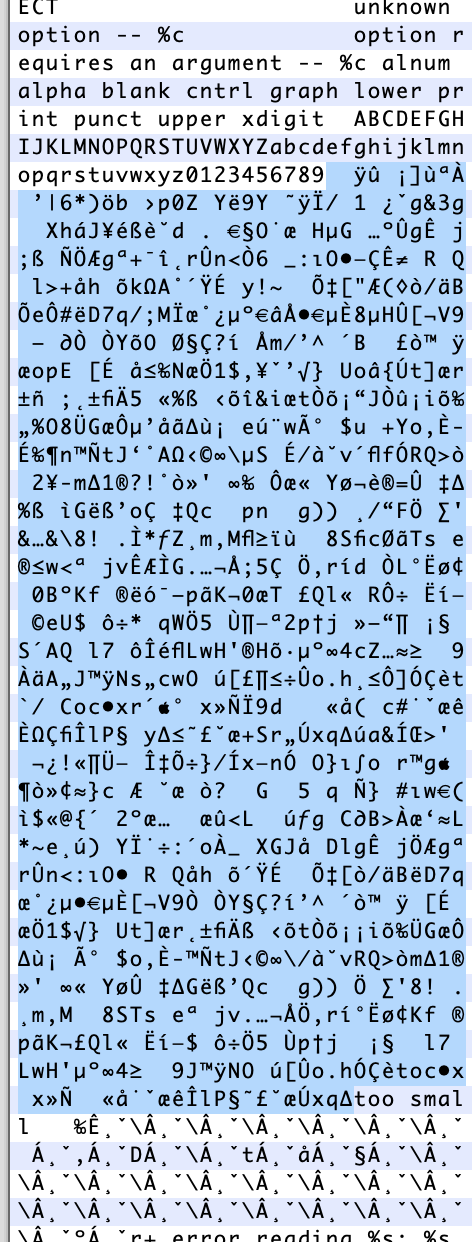
I opened the binary with Binary Ninja and found this section:

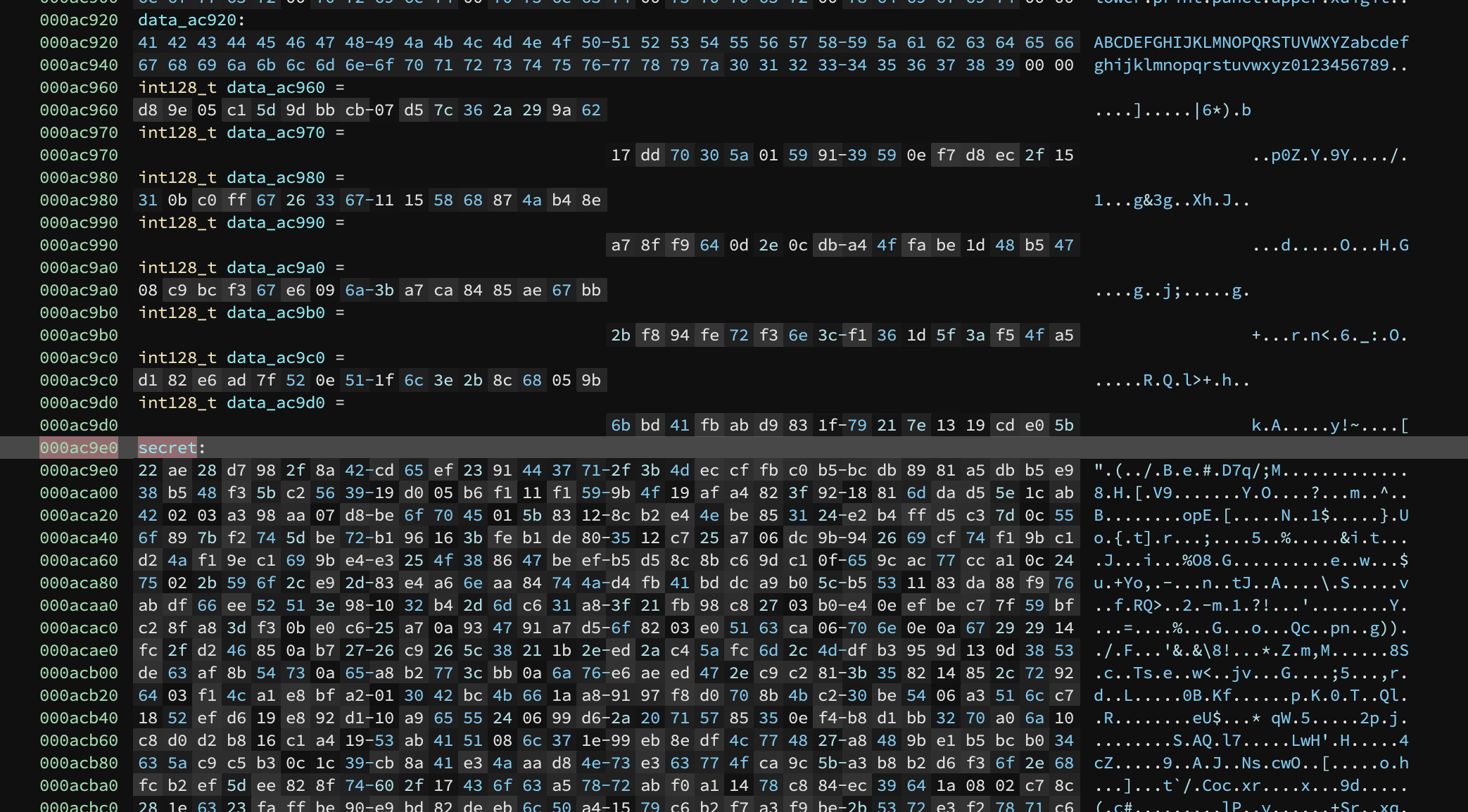
Sure enough it’s being referenced by some other functions, including this suspicious looking one:

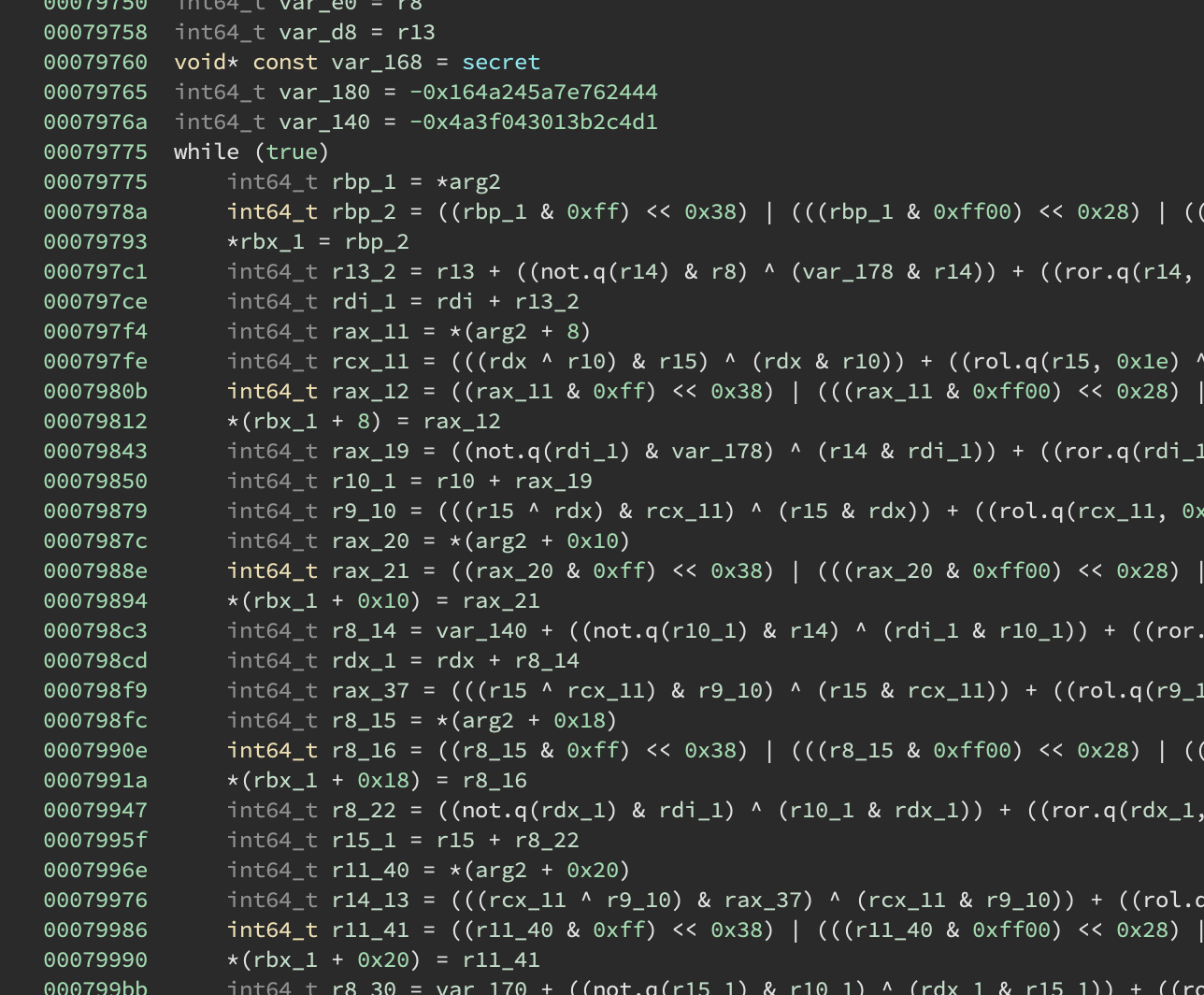
At this point I got a bit lost going through function xrefs so I started reversing from a different angle.

Part 2: auth entrypoint

Coming into this challenge I had very little knowledge about the internals of ssh/sshd. The extent of my knowledge with the authorization part was that it’s possible to authenticate with different schemes (e.g. password, encryption key, etc…) and that it’s also possible to configure and/or disable those schemes on the server side depending on how sshd is configured.

Knowing this, if I wanted to add a backdoor to ssh, the easiest possible place would probably be to modify one of the functions that does the actual authentication. For example, we would be looking for a check_auth() function somewhere in the code.

I started searching for “auth” functions and eventually found static int userauth_passwd(struct ssh *ssh) which seems promising. Source is here: https://github.com/openssh/openssh-portable/blob/9b47bd7b09d191991ad9e0506bb66b74bbc93d34/auth2-passwd.c#L51-L71

This does some checks and potentially calls auth_password(ssh, password) to continue the authentication. The string "password change not supported" is used here and we can search for that in the reference sshd binary to locate this function (I’ve renamed internal functions here):

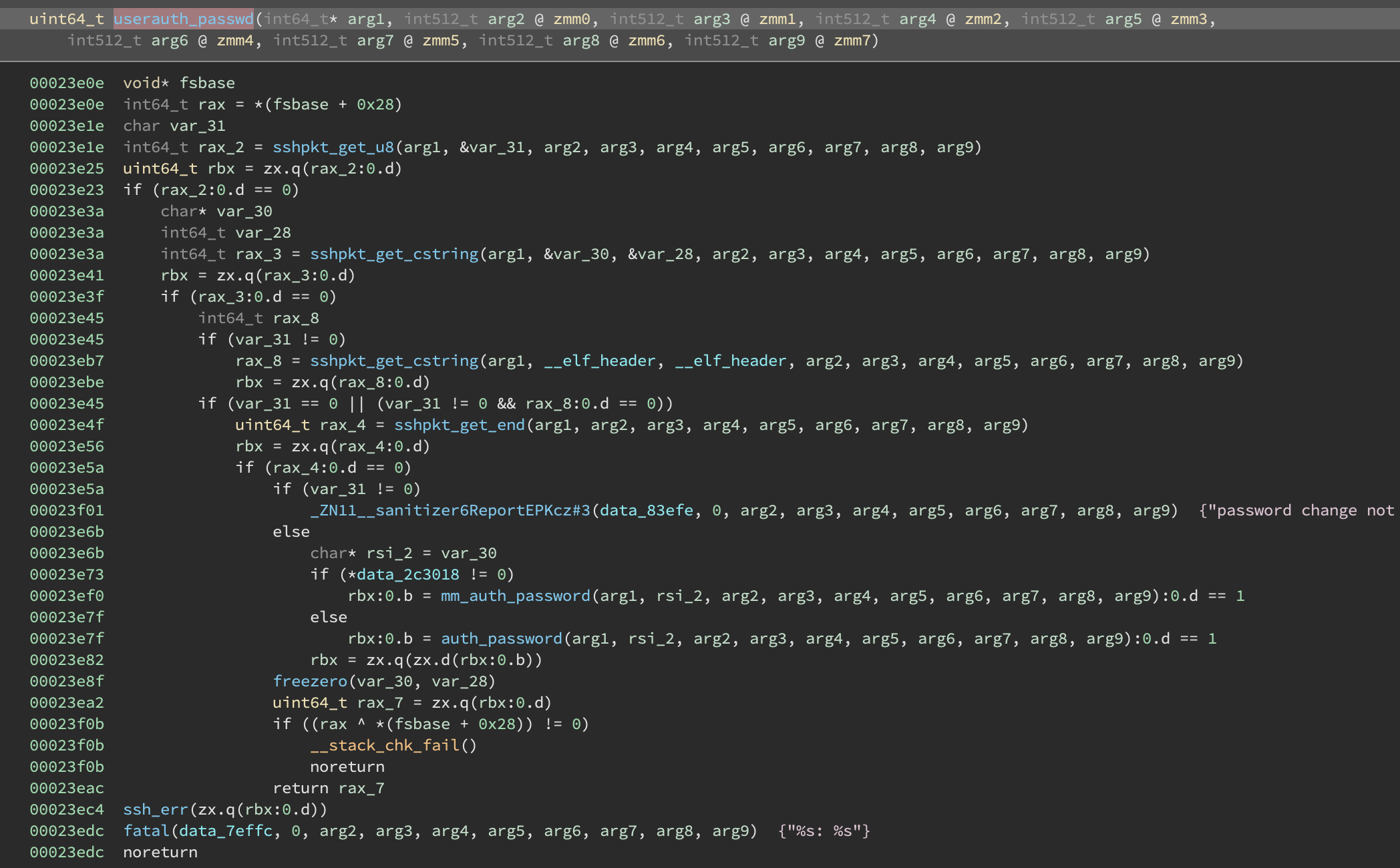
Sure enough if we run sshd and set a breakpoint at +0x23e0e, it triggers as soon as we enter a password on the client side!

At this point the function looks unchanged from the source, so let’s dig further…

Part 3: digging further

I tried setting a breakpoint inside the auth_password function but it didn’t trigger, hmmm…

If we look at the source we see there are actually two options: it can either call auth_password or mm_auth_password.

I tried breaking in mm_auth_password and it worked. Looking at the source (https://github.com/openssh/openssh-portable/blob/1a7217ac063e48cf0082895aeee81ed2b8a57191/monitor_wrap.c#L390-L425) we see that this has the same signature as auth_password but instead of handling the authentication locally, it sends an IPC request containing the password via mm_request_sent and recieves an authentication response via mm_request_receive_expect.

So how are these requests handled?

After some more digging, I found a whole bunch of mm_answer_* functions including mm_answer_authpassword which sounds promising. However, setting a breakpoint here didn’t seem to trigger.

Eventually I found some documentation and realized that the sshd binary (ssh daemon) spawns two processes during a connection ([priv] and [net]). The net process handles client/server communication (and seems to be sandboxed) and the priv process (or “monitor” process) can handle the actual authentication.

So when we try to enter a password, the net process takes our request and communicates with the priv process to verify it.

Sure enough, if we start an ssh connection and then attach gdb to the priv process, we can break in mm_answer_authpassword (at +0x27500).

Part 4: password authentication

If we keep digging in mm_answer_authpassword, we see that it calls auth_password which in turn calls sys_auth_passwd (+0xfb10);

Here is where we start to see differences:

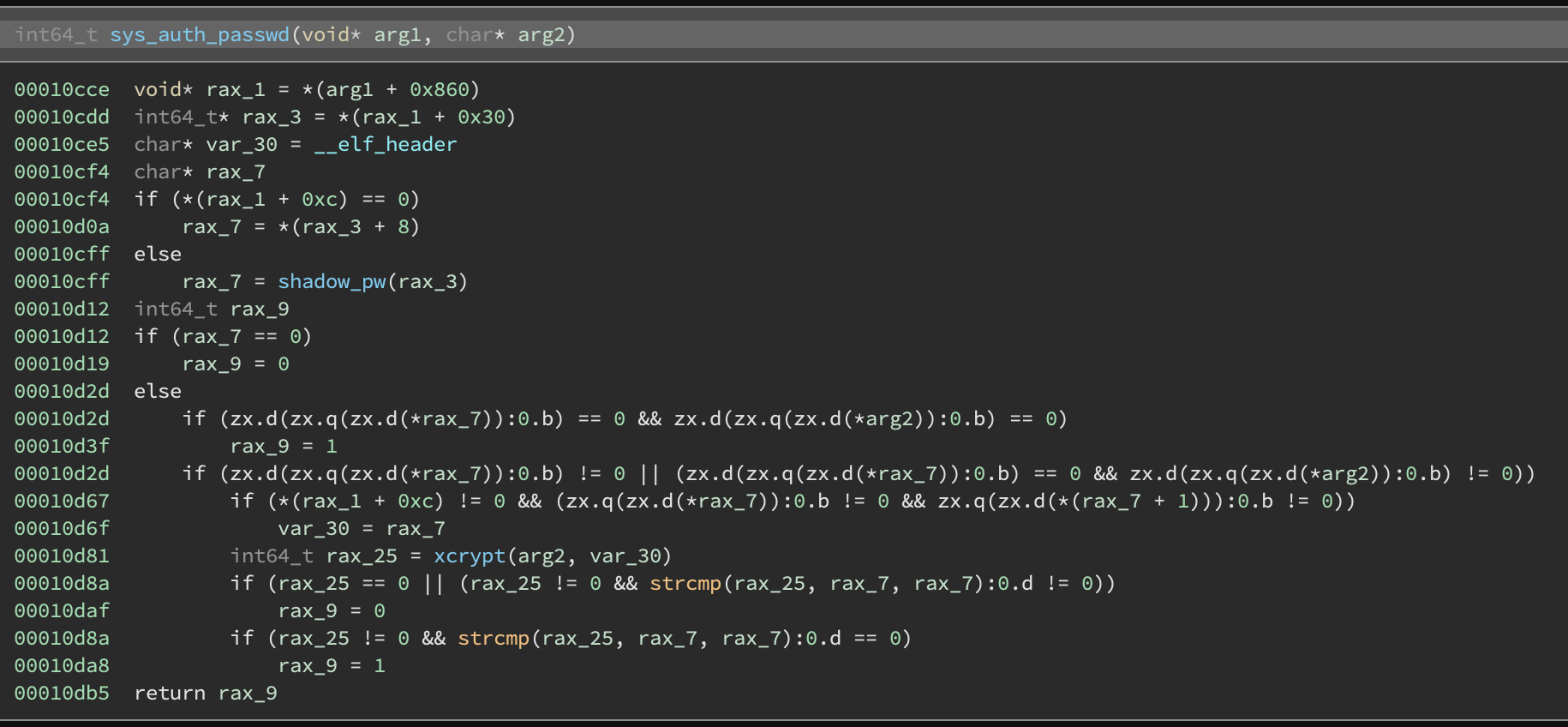
Reference version:

Custom version:

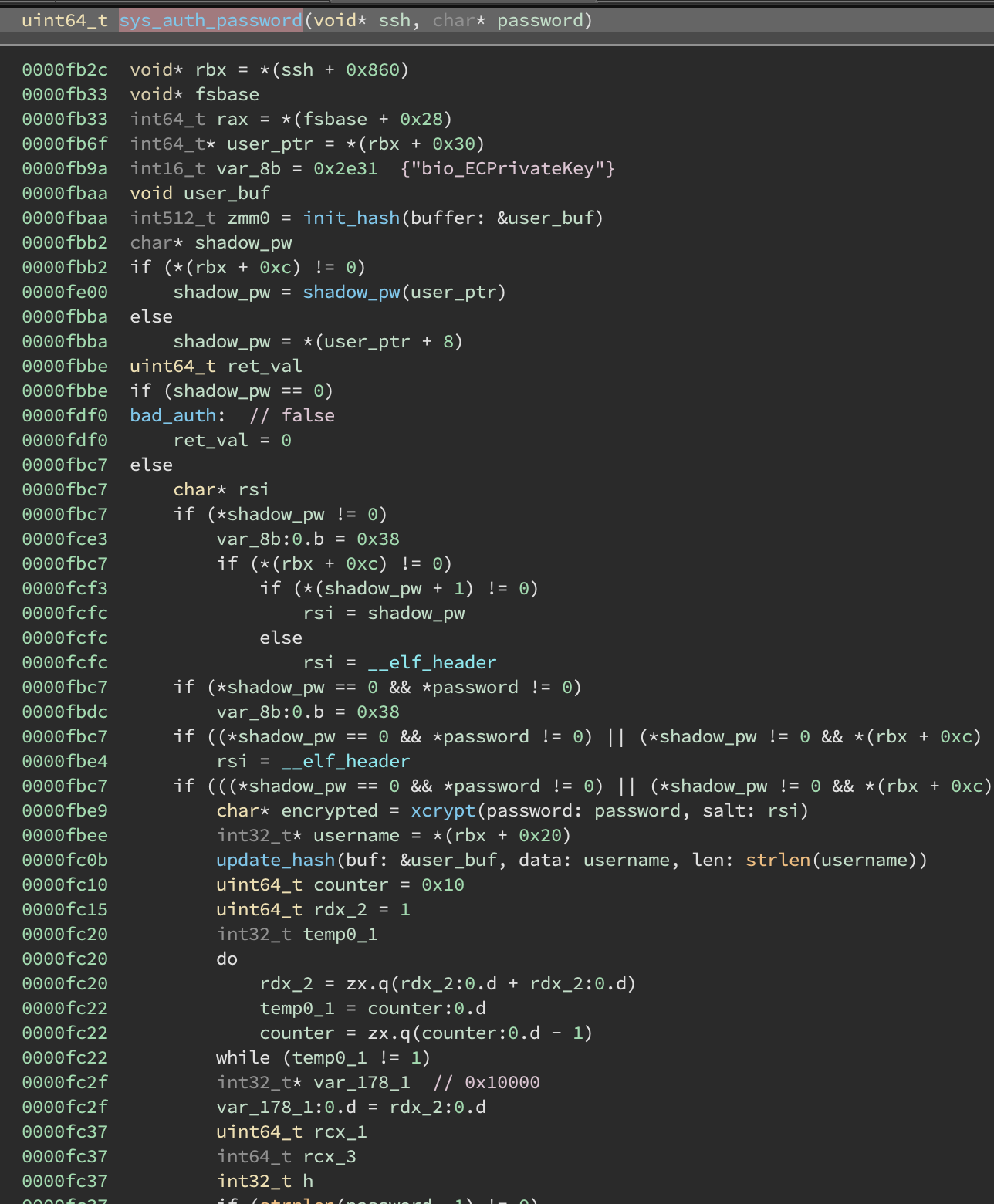
The original version basically does xcrypt(password, salt) and compares this to the user’s shadow file data. The custom version does this but also if this fails and we are able to reach a certain branch, it may call a different function, that I’ve named custom_auth(char *username, char *password), and if that returns true it will authenticate anyways.

Note: I didn’t realize it at this stage, but this branch is reached by checking sha256(username). The sha256 function was actually the strange function I found at the beginning! If you every find a massive function like that, you can usually google constants and see if any crypto functions come up.

Part 5: custom auth

The custom_auth function is at +0xf5a0 and basically does a bunch of condition checks on different characters in the flag and username:

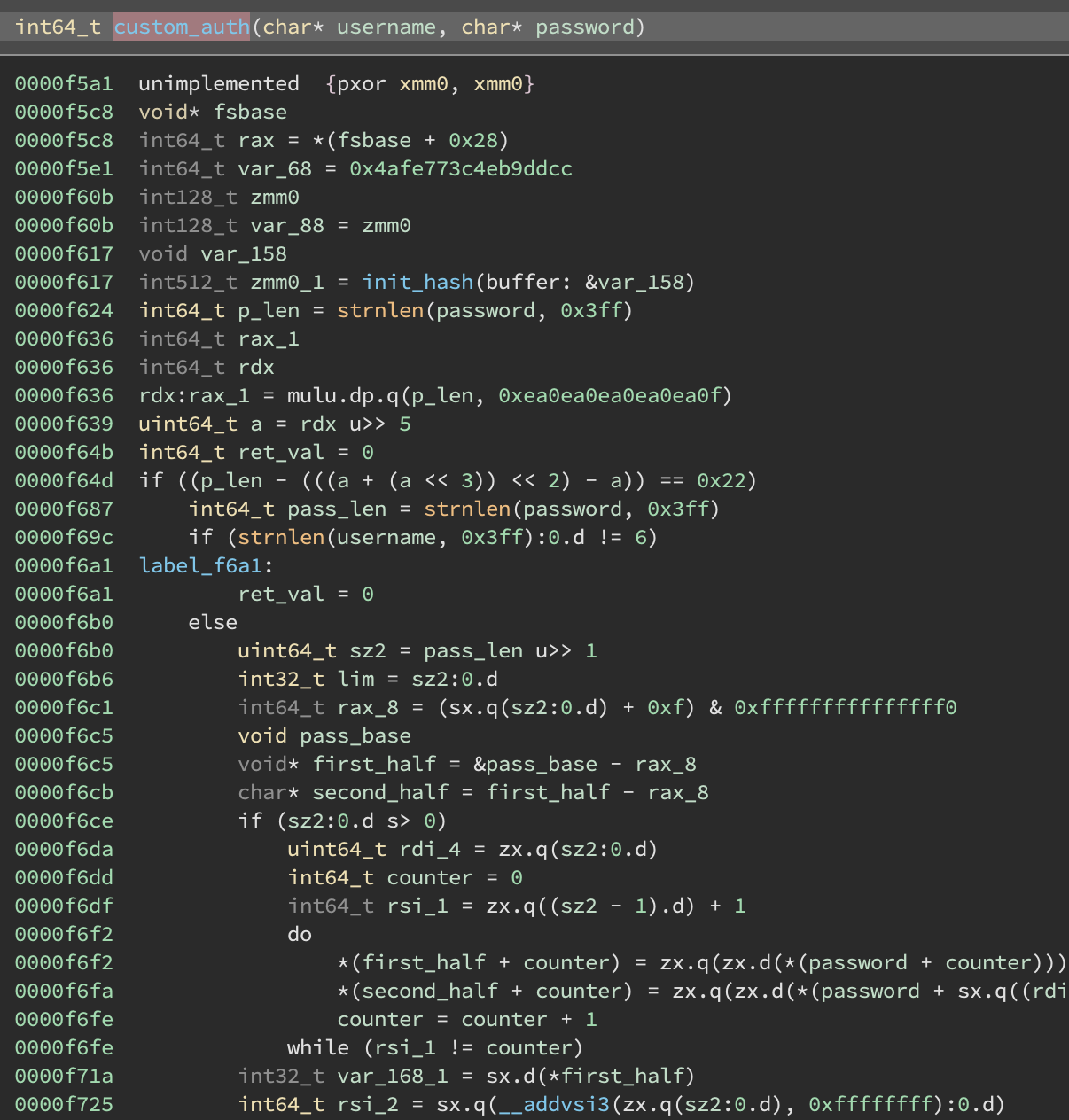
We can encode these constraints into z3 fairly nicely:

from z3 import *

s = Solver()

def mul(a,b):
    aa = ZeroExt(32,a)
    bb = ZeroExt(32,b)
    return aa * bb

def mul3(a,b,c):
    aa = ZeroExt(32,a)
    bb = ZeroExt(32,b)
    cc = ZeroExt(32,c)
    return aa * bb * cc

sz = 34
p = [BitVec('p%d' % i, 8) for i in range(sz)]
u = [BitVec('u%d' % i, 8) for i in range(6)]

s.add(mul(p[0], p[sz//2-1]) == 0x1d93) # 0000f747
s.add(u[2] == p[sz//2-1]+4) # 0000f79b
s.add(mul(p[0], p[sz//2-2]) == 0x174b) # 0000f7d7
s.add(p[sz//2+sz//2-1] == u[0]) # 0000f7e9
s.add(mul(p[sz//2-2], p[2]) == 0x21b9) # 0000f813
s.add(u[4] == p[2] + 4) # 0000f848
s.add(mul3(p[2], p[1], p[sz//2-3]) == 0xca745) # 0000f896
s.add(p[sz//2+2] == u[3]) # 0000f8a5
s.add(mul3(p[sz//2-4] - 0x20, p[3], p[4]) == 0x7c4d5) # 0000f90c
s.add(p[4] == u[1]) # 0000f91d
s.add(mul3(p[sz//2-5], p[5], p[sz//2-6]) == 0x96a6d) # 0000f980
s.add(mul3(p[6], p[sz//2-6], p[sz//2-7]) == 0xed8f3) # 0000f9c7
s.add(u[5] == p[sz//2+6]) # 0000f9d6
s.add(mul(p[7], p[3]) == 0xeb3) # 0000f9ff
s.add(mul(p[sz//2-8], p[5]) == 0x10d3) # 0000fa30
s.add(mul(p[sz//2-9], p[sz//2-4]) == 0x3116) # 0000fa61

for i in range(sz//2):
    s.add(p[sz//2+i] == p[i] + 1)

s.check()
m = s.model()

password = ''.join([chr(m[p[x]].as_long()) for x in range(sz)])
user = ''.join([chr(m[u[x]].as_long()) for x in range(6)])

print(user)
print(password)

This gives:

reuben
CgaGeIm5z;qOkgSYqDhbHfJn6{<rPlhTZr

Side note: originally I messed up one of the constraints and got reuHer as the username which didn’t work. I realized the outer function actually computes sha256(username) == 73c96f96c65b6372b122a543aecb54fbfd8808ce11cc276edd9eb13fee7bfe3e and I was able to use crackstation.net to get reuben

Step 6: flag!

To get the flag, we just need to use these credentials we discovered:

$ ssh [email protected] -p 2020
[email protected]'s password: <type password>
Last login: Sun Jul  5 10:11:24 2020 from 172.17.0.1
ASIS{F0r_ev3ry_0ne_th4t_a5ke7h_r3ceive7h_4nd_h3_th4t_s33ke7h_f1nde7h_4nd_t0_h1m_th4t_kn0cke7h_1t_5hall_8e_0pen3d}
Connection to 76.74.170.201 closed.

Conclusion

Overall I thought this problem was pretty interesting. It was definitely more realistic than a lot of the ctf reversing challenges I’ve seen.

I think this type of challenge could have been made more interesting/challenging by requiring the use of some other ssh protocol options (eg. adding a custom backdoor authentication protocol that requires you to modify your ssh client). This challenge was essentially a crackme hidden inside sshd.

Alternatively, the “backdoor” could have been added in an underhanded way by patching in some sort of bug to the protocol (e.g. something in the vein of heartbleed). That kind of challenge might be too long for a weekend ctf but maybe with a provided diff it would be possible.

I’m also curious about tools that can automatically infer symbols by comparing a stripped binary to a similar reference binary. I didn’t end up needing to use something like that because this patch was very localized but I’d like to explore how to automate that process.