0CTF/TCTF 2020 - sham (733pt)
Neural Network Hash Cracking
June 29, 2020
crypto
ml
sham (733pt, 5 solves)
Crypto
Files:
Overview:
In this challenge we are given the source of a small flask app. The goal is to log in with a valid name and authentication value. The name must start with admin and the authentication value is a 64 byte hash that we need to predict.
task.py
secret_key = os.urandom(0x30)
def get_auth(name):
return hash(secret_key+name)
# ...
@app.route('/login')
def login():
name = request.args.get("name")
auth = request.args.get("auth")
try:
auth = bytes.fromhex(auth)
except:
return "?"
if name[:5] == "admin" and get_auth(name.encode('latin-1')) == auth:
return "lgtm. "+flag
else:
return "?"
@app.route('/register')
def register():
name = "test_"+''.join([random.choice(string.ascii_letters) for _ in range(8)])
auth = get_auth(name.encode('latin-1'))
return "name: "+name+"<br>auth: "+auth.hex()
The hash is implemented with a pytorch module:
class hash_func(nn.Module):
def __init__(self, input_size=64):
super(hash_func, self).__init__()
self.l1 = nn.Conv1d(1, 1, 5, 1, 2)
self.l2 = nn.Conv1d(1, 1, 3, 1, 1)
self.l3 = nn.Linear(64, 32)
def forward(self, input):
x = F.leaky_relu(self.l1(input), 0.2)
x = F.leaky_relu(self.l2(x), 0.2)
x = F.tanh(self.l3(x.view(-1, 64)))
return x
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
H = hash_func().to(device)
H.load_state_dict(torch.load("./param.pkl", map_location=device))
H.eval()
def hash(m):
m = m.ljust(64, b'\x00')
m = list(map(lambda x:float(x-128)/128, m))
x = Variable(torch.Tensor(m[:64]).to(device))
x = x.view(-1, 1, 64)
res = H(x).tolist()
#res = bytes(map(lambda x:int(x*128+128), res[0])) # it will always converge to same char :( not used
bs = map(lambda x:(int(x*32768+32768)//256, int(x*32768+32768)%256), res[0])
res = bytes([y for x in bs for y in x])
return res
Essentially, the 64 byte input is scaled to the range (-1,1) and passed to the network. Each value in the 32 byte output is decoded to produce two byte values.
The difficulty is that out login name is prepended with 48 random bytes so we cant simply compute the hash locally. To leak information about the secret key, we are provided a register function that will give us the hash for random names of the form: test_xxxxxxxx.
To understand the hash function, it helps to visualize how the network is connected (layers shown in the diagram have fewer nodes than in reality):
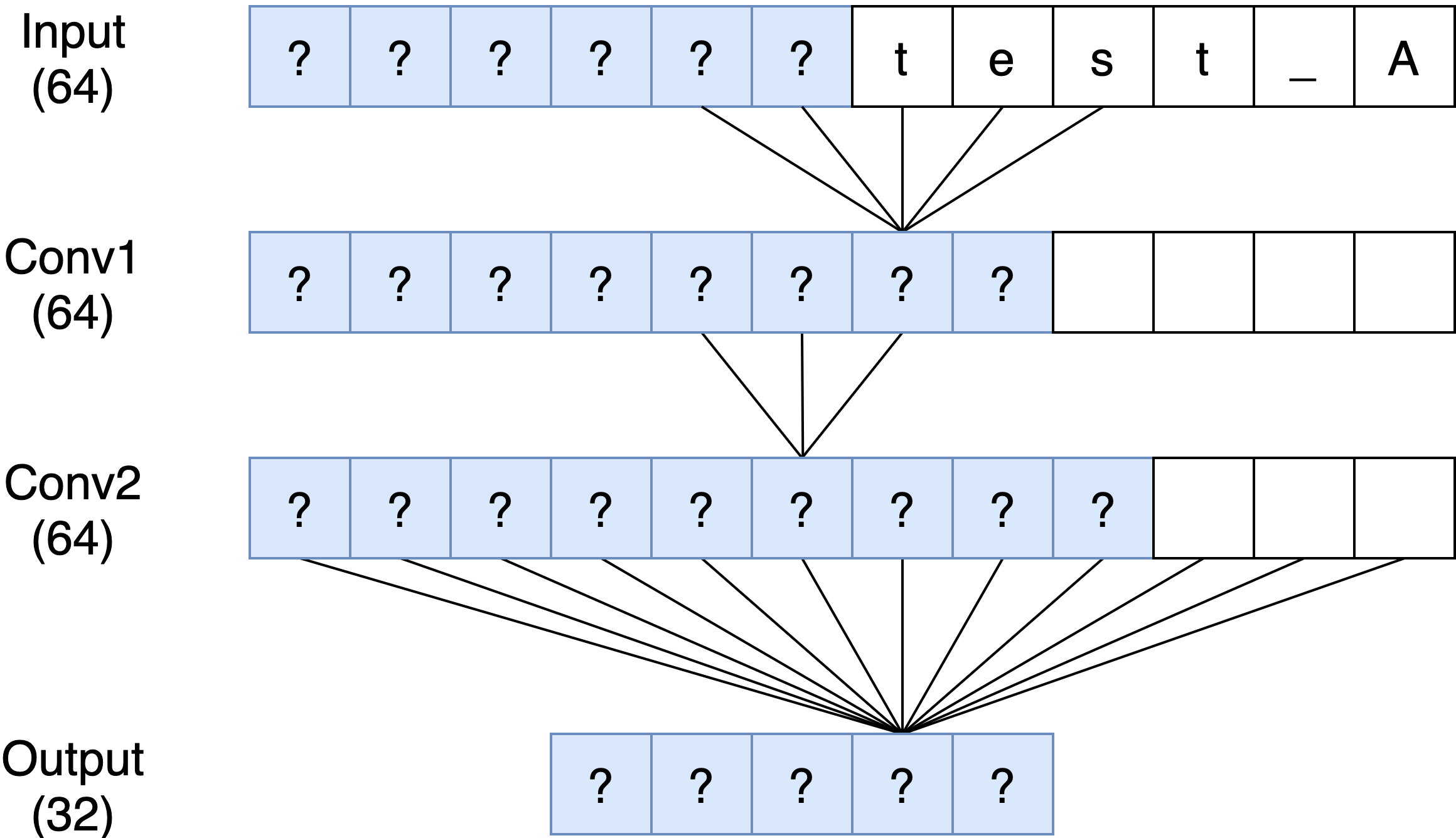
The blue nodes indicate nodes with unknown values. Each conv1d layer is computing a weighted sliding window over the previous layer (sizes 5 and 3 respectively).
I spent close to 15 hours on this problem and tried quite a few different strategies before finding the solution. This writeup outlines my attempts:
(failed) Attempt 1: adversarial attack
My first idea was to try to solve for the key through gradient descent. Essentially, we fix all the weights in the network and try to minimize loss by modifying our current guess for the secret key. In pseudo-code:
secret = Variable(48)
def step_example(name, hash):
# compute prediction
x = (secret + name)
p_hash = H(x)
loss = mse(hash, p_hash)
# gradient descent
secret -= gradient(loss, secret)
Even using thousands of samples, I realized that the key would not converge to the ground truth, rather there were many possible solutions since the key space is so large.
(failed) Attempt 2: reduced adversarial attack
After my first approach, I realized that we don’t actually need to recover the full key, rather we just need to recover the effect of the key on the final output layer.
Here we basically split the final dense layer into three parts: known, partially known and fixed. We can find exact solutions for 15 values after the second convolutional layer (since these values don’t “see” the key at all and hence do not depend on the key values). A similar idea applies to the first 45 values, these values don’t “see” the name at all and are actually fixed. The insight here is that since we will just apply a weighted sum of these 45 values to the output layer, we an reduce it to a single array of unknowns (basically a fixed bias term we add to the output layer).
Finally, there is a portion of the final layer that sees both the key and our (known) name. Here we can perform regression like above, but the number of values we need is reduced to six. In pseudo-code we now have:
secret = Variable(6)
key_weights = Variable(32)
def step_example(name, hash):
# compute prediction
# forward pass on name and bordering part of key
x = (secret + name)
x = leaky_relu(conv1(x), 0.2)
x = leaky_relu(conv2(x), 0.2)
x = W3[:,45:] * x # partial application of dense layer
x = (x + key_weights + B3) # add key weights and bias
p_hash = tanh(x)
loss = mse(hash, p_hash)
# gradient descent
secret -= gradient(loss, secret)
key_weights -= gradient(loss, key_weights)
With this approach, I was able to get close to 80% accuracy on unseen values. However, it was clear that the values were not converging to the ground truth.
Attempt 3: delta forward pass
After some sleep, I came back to this problem from a different angle. Instead of trying to produce a valid hash, why don’t we thing about mutating a hash into a target.
For example, we can think about what happens when we mutate the first letter of our hash for test_ABCDEFGH into aest_ABCDEFGH. Here, the effect of the value in the input layer is -0.1484375. So how does this affect other layers? Well we can actually perform a forward pass with this value to see the effect:
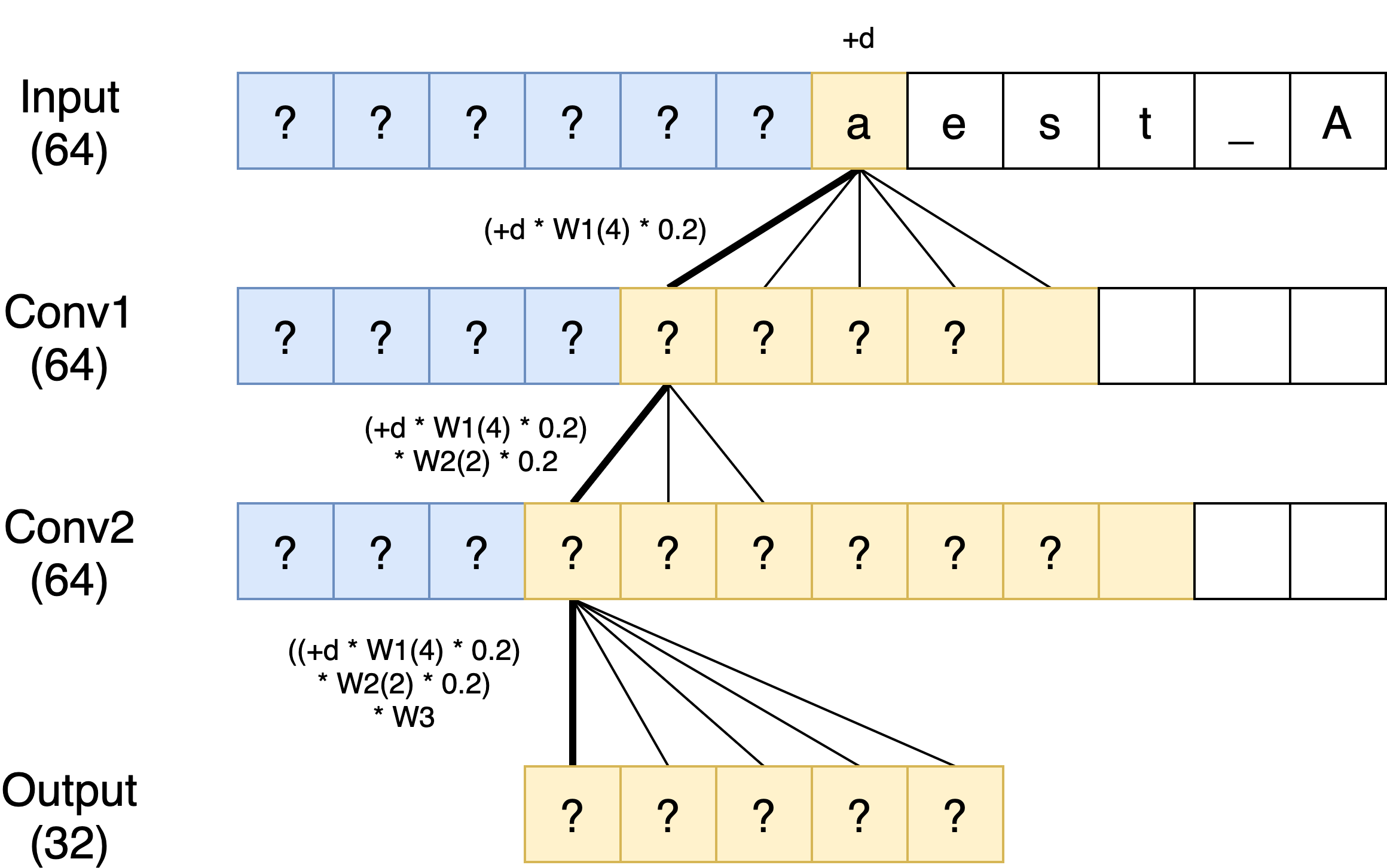
Now there is one issue: when we mutate a value that goes through leaky relu, we don’t actually know if the value is on the positive or negative side (or if it would cross zero). So how can we figure out the activation to apply? Well it turns out that for whatever reason pretty much all the values in the first two conv layers are negative and so this makes our job easy. We can simply apply the activation of x * 0.2 as if our value was negative going through the leaky relu.
Using this technique with the mutation from test_ to admin we can essentially compute a “transformation vector” that we can add to any of our “test_” hashes to obtain a valid hash for adminxxxxxxxx.
In practice however, we end up running into a lot of precision errors due to the way integer values are truncated in the hash output. To reduce the precision error, I computed the target mutation from test_xxxxxxxx to admin88888888 for 50 different sampled (name,hash) tuples and averaged the final target hash. This gave me a hash that had one or zero errors most of the time and it is possible to iterate over each byte index and try +/- 1 to obtain the correct hash.
Final solution is here:
import tqdm
import numpy as np
import requests
import time
import binascii
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class hash_func(nn.Module):
def __init__(self, input_size=64):
super(hash_func, self).__init__()
self.l1 = nn.Conv1d(1, 1, 5, 1, 2)
self.l2 = nn.Conv1d(1, 1, 3, 1, 1)
self.l3 = nn.Linear(64, 32)
H = hash_func()
H.load_state_dict(torch.load("./param.pkl"))
W1 = H.l1.weight.detach().numpy()[0][0]
W2 = H.l2.weight.detach().numpy()[0][0]
W3 = H.l3.weight.detach().numpy()
B1 = H.l1.bias.detach().numpy()[0]
B2 = H.l2.bias.detach().numpy()[0]
B3 = H.l3.bias.detach().numpy()
R = 'http://pwnable.org:10002'
# R = 'http://localhost:8080'
def get_remote():
while (True):
try:
r = requests.get(f'{R}/register')
t = r.text
n = t.split('name: ')[1].split('<')[0]
h = t.split('auth: ')[1]
h = binascii.unhexlify(h)
break
except:
print('delay')
time.sleep(1)
return n,h
def test(name, auth):
r = requests.get(f'{R}/login', params={
'name': name,
'auth': auth
})
t = r.text
return t
def conv_delta(buf):
'''delta forward pass assuming negative
leaky relu activation'''
r1 = [0] * (len(buf) + 4)
for i in range(len(buf)):
for j in range(5):
r1[i+j] += (buf[i] * W1[4-j] * 0.2)
r2 = [0] * (len(r1) + 2)
for i in range(len(r1)):
for j in range(3):
r2[i+j] += (r1[i] * W2[2-j] * 0.2)
return r2
def get_transform(a,b,off):
def get_delta(a,b):
a = (a-128)/128.0
b = (b-128)/128.0
return (b - a)
# compute change in input
delta = [get_delta(x,y) for x,y in zip(a, b)]
d = conv_delta(delta) # forward pass
hash_shift = np.matmul(W3[:,off:off+len(delta)+6], d)
return hash_shift
def hash_to_out(h, c):
o = []
for i in range(0,len(h),2):
v = ((h[i] * 256) + h[i+1]) + c
v = (v - 32768) / 32768.0
o.append(v)
return o
def out_to_hash(out,c):
v = out*32768+32768 + c
r = []
for i in range(32):
r.append(v[i] / 256.0)
r.append(v[i] % 256.0)
v = np.round(v)
bs = map(lambda x:(int(x)//256, int(x)%256), v)
res = bytes([y for x in bs for y in x])
return res
def enumerate_hash(byt):
p = []
for i in range(1,len(byt),2):
bc = list(byt)
bc[i] += 1
p.append(bytes(bc))
bc = list(byt)
bc[i] -= 1
p.append(bytes(bc))
return p
# ---
N = 50
keys = []
for i in tqdm.tqdm(range(N)):
keys.append(get_remote())
time.sleep(1)
# predicted hash
pr = np.zeros(32)
for i in range(N):
t = get_transform(keys[i][0].encode('latin-1'), b'admin88888888', 45)
o = np.arctanh(hash_to_out(keys[i][1], 0.5))
p = np.tanh(o + t)
pr += p
pr /= N
# try current prediction
h = out_to_hash(pr, -0.5)
print(test('admin88888888', binascii.hexlify(h)))
# try flipping each byte by 1
for p in tqdm.tqdm(enumerate_hash(h)):
print(test('admin88888888', binascii.hexlify(p)))
time.sleep(1)
# flag{i5_1t_S0_ca1l3d_forWard_pRopAga7ion??????????}