PlaidCTF 2021 - minipokemon (450pt / 12 solves)
Pokemon Mini ROM reversing.
April 18, 2021
s1c88
rev
minipokemon
Description:
Enter the world of minipokemon!
Director: ubuntor
Cast: tylerni7
Files:
Overview
We are given a file called “minipokemon.min”. After a quick google, we can see that this is a ROM file for the Pokemon Mini.
The Pokemon Mini is a handheld game console running the S1C88 CPU. Here’s a manual.
1. First Steps
Before this challenge I had never heard of the S1C88 architecture or even the Pokemon Mini. So I spent a fair bit of time reading the introduction in the maual linked above.
I’ll give a brief intro to the architecture here:
Registers
There are only a few registers:
BA(16-bit),B(8-bit),A(8-bit)HL(16-bit),H(8-bit),L(8-bit)IX(16-bit)IY(16-bit)PC(16-bit) (program counter)SP(16-bit) (stack pointer)XP(8-bit)YP(8-bit)
Memory
Memory is banked so the first 0x8000 bytes are mapped to physical page 0 while the upper half of memory is mapped to the page specified by the 8-bit BR register (this ends up not being used).
Instructions
The instructions are Chip-8-like and mostly interpretable if you’re familiar with other 8-bit architectures.
LD a,b: mov between two points, there are many addressing modes, for example:LD A,BLD [HL],ALD [0x1234],ALD L,[0x4566]LD B,[IX+0x20]
ADD/OR/XOR/SUB/MUL/INC/DEC: math operatorsCP a,b: compare two values and set flagsCARL: a call instructionJRL/JRS: jump long/short, this can also be conditionalRET/RETE: return from function and interruptDJR: decrement and jump if not zero (like x86 loop)
2. Disassembly
I typically use Binary Ninja for reversing problems and unfortunately there was no S1C88 plugin. So I decided to make one. I spent several hours with ehennenfent writing a disassembler plugin (with LLIL lifting!).
You can get it here: https://github.com/hgarrereyn/bn-pokemon-mini.
This gives us nice graphs like:
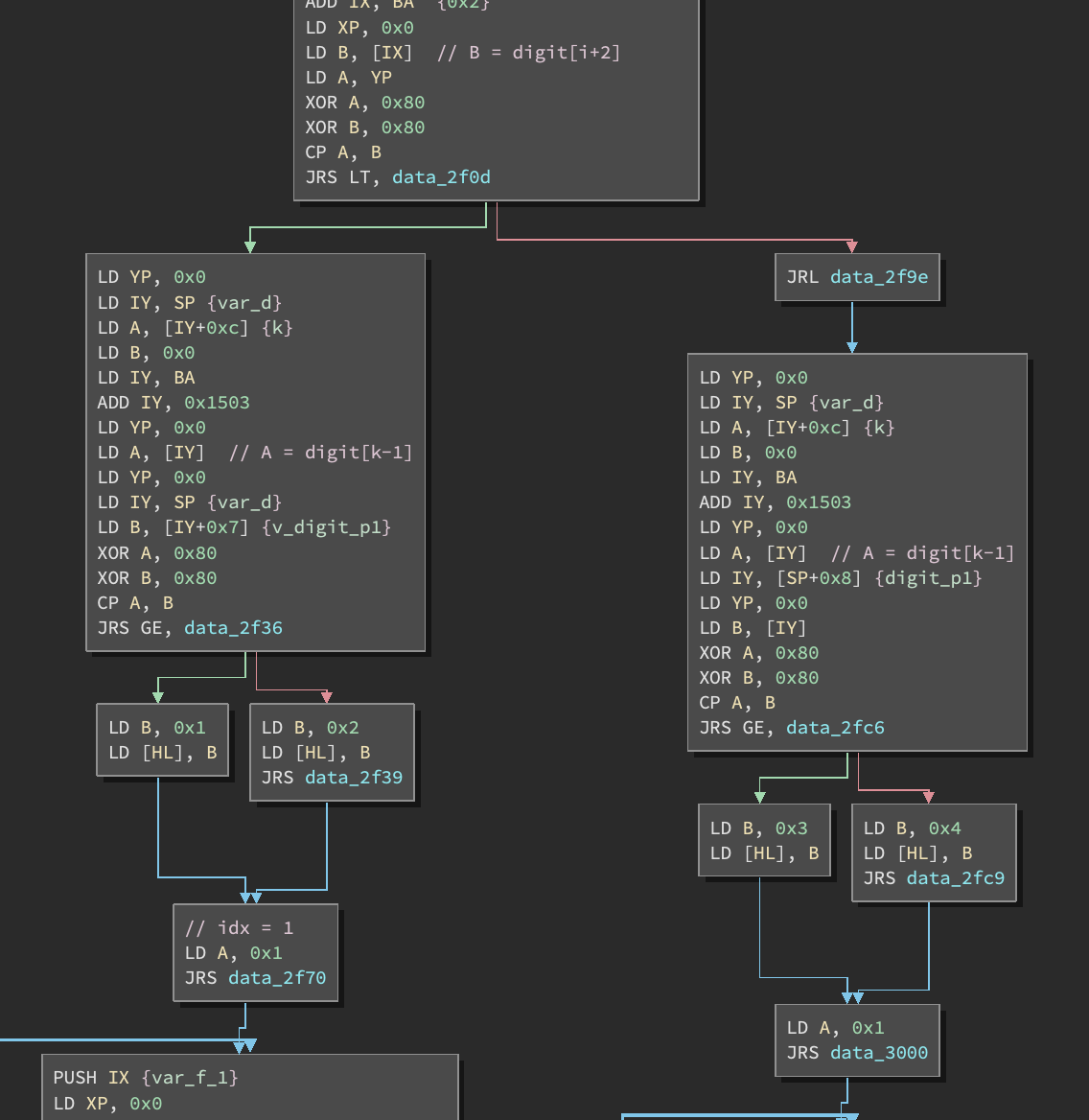
3. Reversing
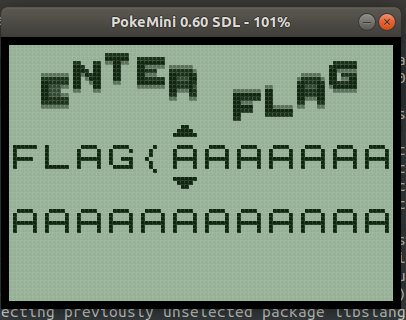
The program itself is a simple flag checker. You enter a 24-character flag by moving a cursor left and right over the current string and incrementing and decrementing characters. When you press A it will check the flag and print out a “correct” or “incorrect” message.
Button presses are handled as interrupts in the S1C88. Due to ehennenfent adding symbols to the binary view, we were able to quite clearly see where those functions were called:

After reversing the interrupt handlers we were able to figure out where the input was stored in memory. Specifically, the program used a 5-line buffer like the following:
0x1380: ^
0x1390: FLAG{AAAAAAA
0x13a0: v
0x13b0: AAAAAAAAAAA
0x13c0:
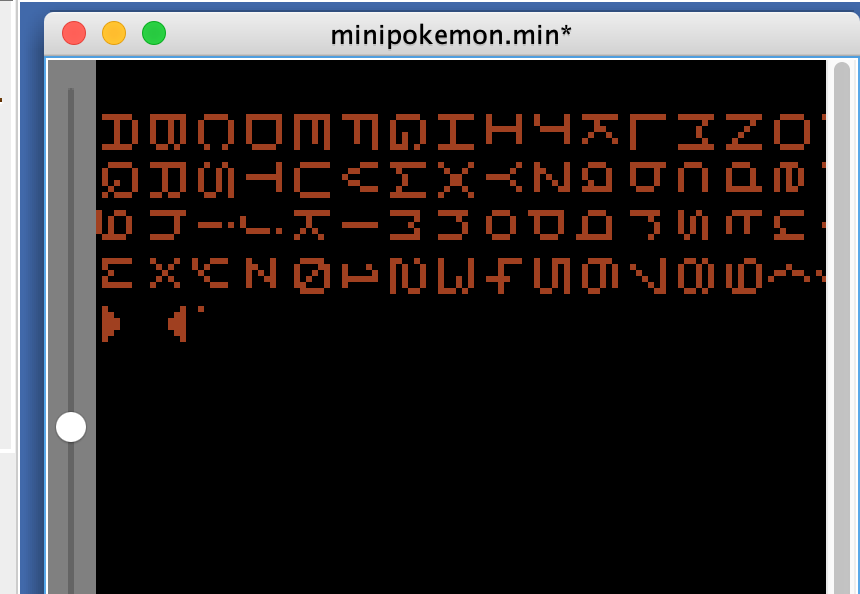
Each line represents the current text draw on the screen. Graphics are handled by the PRC (program rendering chip). Specifically, the buffer here contains sprite indexes which are rendered as a map tileset with the tileset at 0x10000 which is simply an alphabet:
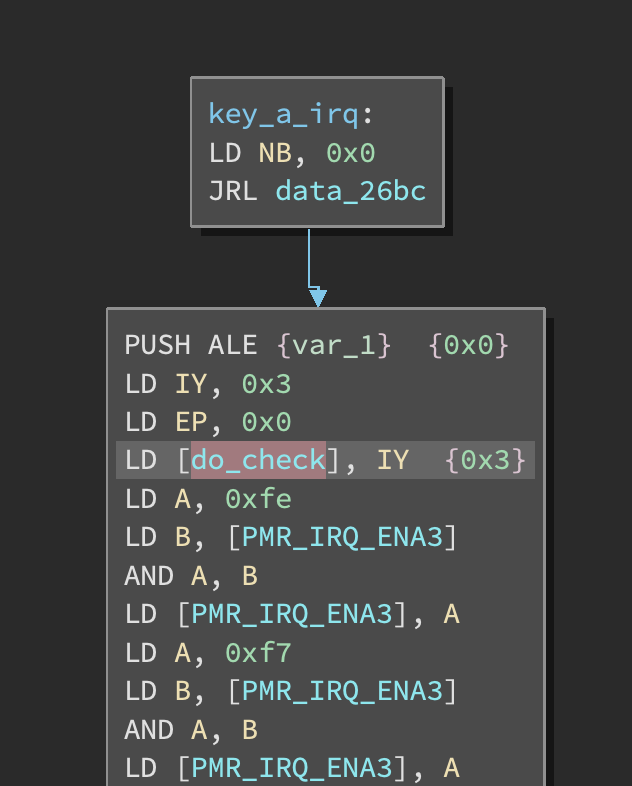
In the function handler for the “A” keypress, we see the following flag set:
Inside the main function, we see that it spinlocks on this flag:
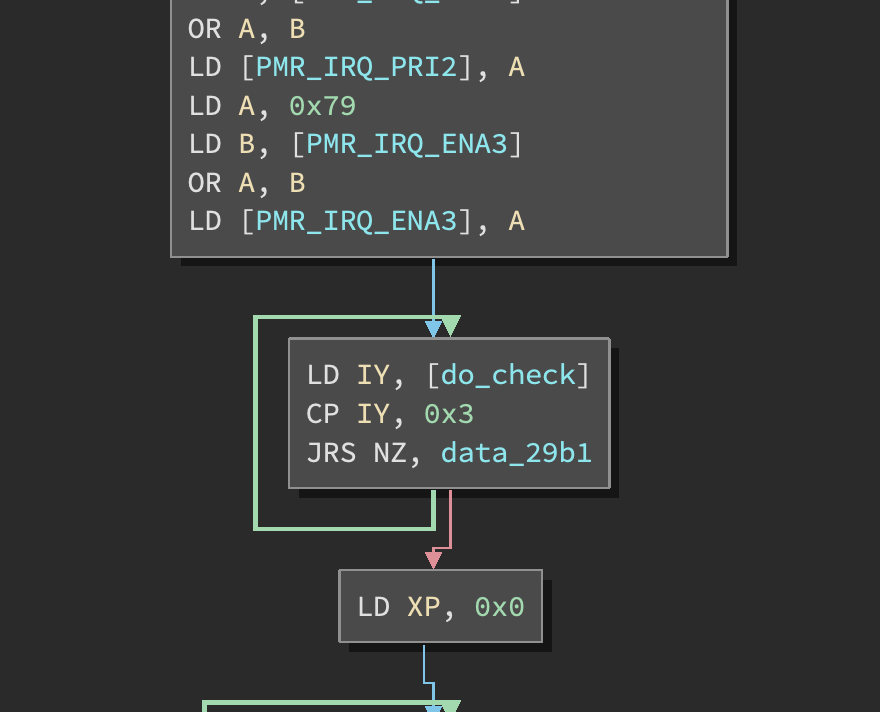
Afterwards it calls a check_flag function and takes one of two control paths (presumably printing either “correct” or “incorrect”).

The check_flag function (shown above) is a fairly massive piece of code and it took quite some time to reverse. The main control flow consists of 5 separate sections. In each section there are some conditionals that may cause it to exit with a failure case.
In short the check_flag function does the following:
- XOR user input with a magic string
- Convert the result to decimal and produce a large digit array that is interpreted as pairs of coordinates:
[x0,y0,x1,y1,...,xn,yn] - Neighboring coordinates can’t share values
x[i] != x[i+2]andy[i] != y[i+2] - Each consecutive pair of coordinates
x1,y1andx2,y2specifies a line fromx1,y1tox2,y1tox2,y2. Horizontal edges in the line are stored as value5in a path array while vertical edges are stored as6. Corners in this path are stored as1-4depending on the orientation. - If any component of the path is self-intersecting, the check fails.
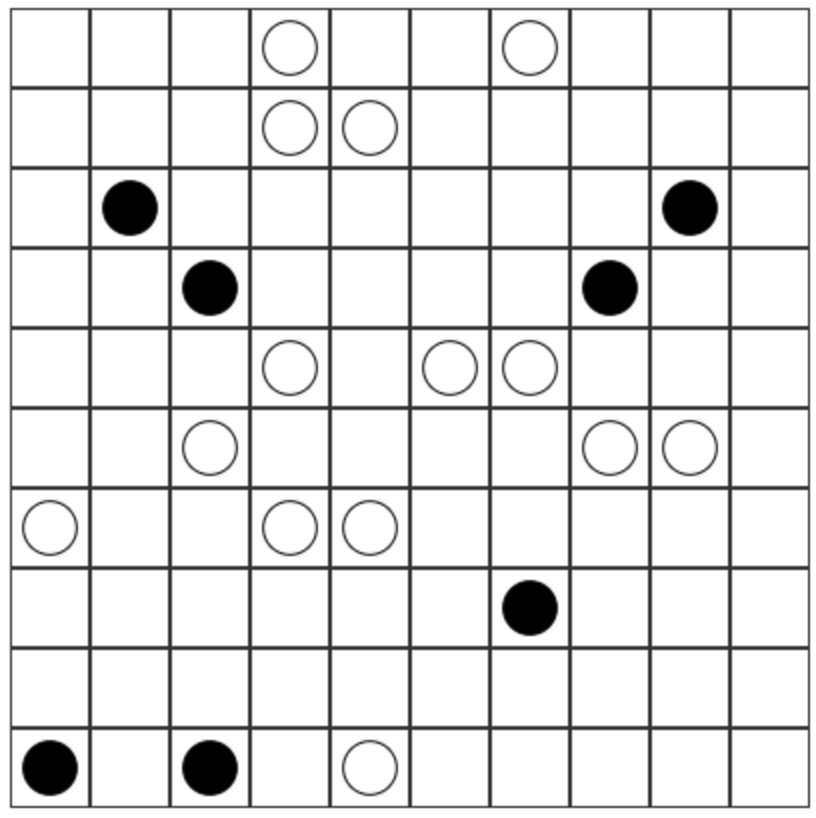
- The path is validated using Masyu rules. Specifically there is a specified set of corner points (black dots) and edge points (white dots). Black dots must lie on a corner, white dots must lie on an edge and neighbor a corner:
The solution is obtained with the following path:
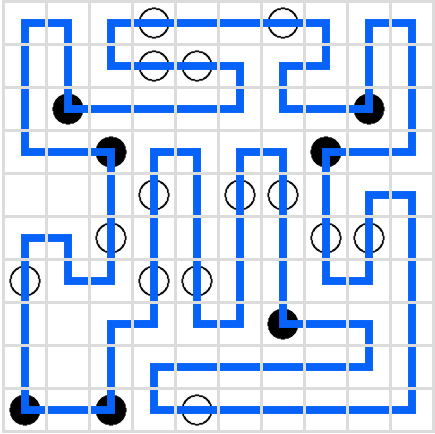
I’ve included a full python implementation of the flag checker at the end of this writeup.
To get the flag, we need to convert this path to a series of coordinates and then reverse the digit construction scheme:
magic = bytes([
15,57,42,9,53,58,
0,59,51,10,33,3,
58,58,17,12,60,60,
13,60,13,0,9,54])
charset = b'\
ABCDEFGHIJKLMNOPQRSTUVWXYZ\
abcdefghijklmnopqrstuvwxyz\
0123456789{}'
def decode(arr):
d_str = ''.join([str(x) for x in arr])
d = int(d_str[::-1])
parts = [0] * 24
for i in range(24):
parts[i] = d & 0x3f
d >>= 6
parts = parts[::-1]
out = bytes([a^b for a,b in zip(parts, magic)])
a_out = bytes([charset[x] for x in out])
return a_out
decode([
1,4, 0,0, 2,2, 3,6, 4,2, 5,6,
6,2, 8,1, 3,0, 9,5, 8,3, 7,6,
9,9, 8,7, 6,8, 7,9, 2,8, 5,7,
1,9, 0,6, 2,3])
"PCTF{5EEth4tFURR3Tw4lcc}"
Entering this in the original game reveals the furret:
now that plaidctf is over i can finally share this furret (with 1-bit accumula town music) pic.twitter.com/dJmHN548P2
— /^\/j?ub⦋uʌ⦌nt(ɔɹ|ɚ)\/$/ (@ubuntor) April 18, 2021
Timeline
I’ve included a timeline of the reversing process (including parts where we got stuck and deadends). Usually CTF writeups are just a highlight of the good parts but this should be an accurate description of exactly what steps we took:
(Times are in EST)
- 8:00 PM - Started working on the problem. Lots of searching, figured out the cpu version and started looking for disassemblers.
- 8:30 PM - Tried using mindis2 to disassemble which produced good looking instructions.
- 9:00 PM - After looking through the mindis2 output for a while, started working on a Binary Ninja plugin.
- 9:30 PM - Repurposed the mindis2 instruction encodings to get instructions displayed in Binary Ninja (no LLIL yet).
- 12:30 AM - Most instructions lifted in Binary Ninja. ehennenfent starts working on adding a binary view with symbols for known addresses.
- 2:00 AM - ehennenfent adds binary view support for Pokemon Mini ROMs.
- 3:00 AM - Fixed up a few instruction lifting details, plugin is mostly complete. We start trying to figure out how to emulate the ROM.
- 3:20 AM - We identify some tilesets present in the rom at addresses
0x10000and0x20000. - 3:45 AM - ehennenfent gets the ROM running in an emulator. We start reversing the control flow.
- 4:00 AM - After finding the key control interrupts, we figure out where the flag input data is stored in memory.
- 4:20 AM - ehennenfent gets a debugger running.
- 4:25 AM - We identify
0x2c95as the “flag checker” function and start going through it in detail. - 4:35 AM - Flag input is xored with a magic string.
- 5:20 AM - We figure out that it does hex -> decimal conversion and stores the digits in a separate array.
- 5:40 AM - Consecutive digit constraint.
- 5:50 AM - Brief discussion about getting symbolic execution or fuzzing working.
- 6:20 AM - 2:00 PM - Asleep
- 2:10 PM - Setup a
z3script with the constraints we’ve identified. - 3:00 PM - Identify the first big loop that fills out the coordinate array (we don’t fully realize that these are coordinates by this point).
- 3:15 PM - ehennenfent finds a typo in the C1S88 manual regarding flag conditions.
- 3:30 PM - Get the coordinate array implemented in the z3 script.
- 4:30 PM - Get the corner checker part impelmented in z3. Realize that the z3 script is going to be way too slow (too many symbolic array lookups).
- 5:30 PM - Finally realize that it’s tracing a path in a 10x10 array based on coordinates you provide.
- 5:50 PM - Post a graph of the magic coordinates in discord.
- 6:20 PM - Realize that some of the target points are corner constraints while some are edge constraints. At this point we mistakenly think the edge constraints can’t neighbor a corner on either side while in reality they have to neighbor a corner.
- 6:30 PM - Post a new graph in discord and jschnei immediately identifies it as a Masyu puzzle.
- 6:35 PM - Aplet123, chaosagent and falafel2222 start helping with the puzzle component.
- 7:30 PM - Some progress on the puzzle, but due to the edge constraint mistake, the puzzles are too constrained.
- 8:30 PM - falafel2222 realizes that solving with regular Masyu rules obtains a unique solution of the right size.
- 9:00 PM - After fiddling around with coordinate permutations we finally solve!
In total, we spent 7 hours writing the Binary Ninja plugin, 8 hours reversing the program itself and 2.5 hours solving the puzzle.
Python version
Here is more-detailed, python equivalent code for the flag checker:
magic = bytes([
15,57,42,9,53,58,
0,59,51,10,33,3,
58,58,17,12,60,60,
13,60,13,0,9,54])
charset = b'\
ABCDEFGHIJKLMNOPQRSTUVWXYZ\
abcdefghijklmnopqrstuvwxyz\
0123456789{}'
def check_flag(inp):
# inp is a bytestring like "AAA..."
# convert from hex to index
x = bytes([charset.index(a) for a in inp])
# xor with magic string
x = bytes([a^b for a,b in zip(x, magic)])
# convert to digit array
val = 0
for j in range(len(x)):
val <<= 6
val += x[j]
s_val = str(val)
if len(s_val) > 42:
# flag is too big (numerically)
return False
s_digit = str(s_val).zfill(42)[-42:][::-1]
digits = [int(x) for x in s_digit]
# digits are interpreted as coordinate pairs:
# (x0,y0,x1,y1,x2,y2,...,xn,yn)
# copy two coordinates
digits += digits[:4]
# duplicate coordinate constraint
for i in range(0,42,2):
if digits[i] == digits[i+2]:
return False
if digits[i+1] == digits[i+3]:
return False
# first coordinate must be the smallest
# (this is coord[1] for some reason...)
p0 = (digits[2] * 10) + digits[3]
for i in range(2,44,2):
if (digits[i+1] * 10) + digits[i] < p0:
return False
if (digits[i+1] * 10) + digits[i+2] < p0:
return False
# trace coordinates in the 10x10 array
path = [[0]*10 for i in range(10)]
for i in range(2,44,2):
y0 = digits[i-1]
x1 = digits[i]
y1 = digits[i+1]
x2 = digits[i+2]
y2 = digits[i+3]
# no collisions
if path[y1][x1] != 0: return False
# corner map:
#
# 1,2,3,4 are corners
# 5,6 are edges
#
# 6 6
# 6 6
# 553 155
#
# 554 255
# 6 6
# 6 6
# trace x-component of line
if x1 < x2:
# right
path[y1][x1] = (
1
if y1 > y0 else
2
)
for i in range(1,x2-x1):
if path[y1][x1+i] != 0:
return False
path[y1][x1+i] = 5
else:
# left
path[y1][x1] = (
3
if y1 > y0 else
4
)
for i in range(1,x1-x2):
if path[y1][x1-i] != 0:
return False
path[y1][x1-i] = 5
# trace y-component of line
if y1 < y2:
# up
path[y1][x2] = (
2
if x1 > x2 else
4
)
for i in range(1,y2-y1):
if path[y1+i][x2] != 0:
return False
path[y1+i][x2] = 6
else:
# down
path[y1][x2] = (
1
if x1 > x2 else
3
)
for i in range(1,y1-y2):
if path[y1-i][x2] != 0:
return False
path[y1-i][x2] = 6
# check for target coordinates
corners = [0,0,2,0,6,2,2,6,7,6,1,7,8,7]
edges = [
4,0,0,3,3,3,4,3,2,4,7,4,8,4,
3,5,5,5,6,5,3,8,4,8,3,9,6,9]
# check corners
for i in range(0,len(corners),2):
x,y = corners[i:i+2]
if path[y][x] == 1:
# bottom left
if path[y][x+1] != 5: return False
if path[y-1][x] != 6: return False
elif path[y][x] == 2:
# top left
if path[y][x+1] != 5: return False
if path[y+1][x] != 6: return False
elif path[y][x] == 3:
# bottom right
if path[y][x-1] != 5: return False
if path[y-1][x] != 6: return False
elif path[y][x] == 4:
# top right
if path[y][x-1] != 5: return False
if path[y+1][x] != 6: return False
else:
return False
# check edges
for i in range(0,len(edges),2):
x,y = edges[i:i+2]
if path[y][x] == 5:
# horizontal
if path[y][x-1] == 5 and path[y][x+1] == 5:
return False
elif path[y][x] == 6:
# vertical
if path[y-1][x] == 6 and path[y+1][x+1] == 6:
return False
else:
return False
return True