Overview

This was a challenge from a very short (6 hour) CTF run by Samsung. I played with DiceGang and we got 7th place. There were a few interesting challenges.

It took me about 2 hours to solve this challenge and I ended up reversing the entire thing by hand. I learned afterwards that there was a much easier solution (that required guessing at an xor operation). Additionally, I was kindly informed by meow on redpwn that this is actaully a well-documented esolang called “Legit” 🤦.

During the competition, I did not realize this was an existing esolang so I ended up guessing how most of the operations worked. While it is certainly less efficient doing everything blind, I had a lot of fun and I decided to writeup this “hard way” because I think it is an interesting process.

Legitimate (240pt)

Files:

• yes.tar.gz (downloaded from site, contains .git directory)

This challenge was classified as web and coding and the challenge description links to a website. In the end it turned out to be entirely rev. My teammates started on this challenge before me and found a .git folder stored on the web server. Looking through the commit history, we can see some interesting patterns:

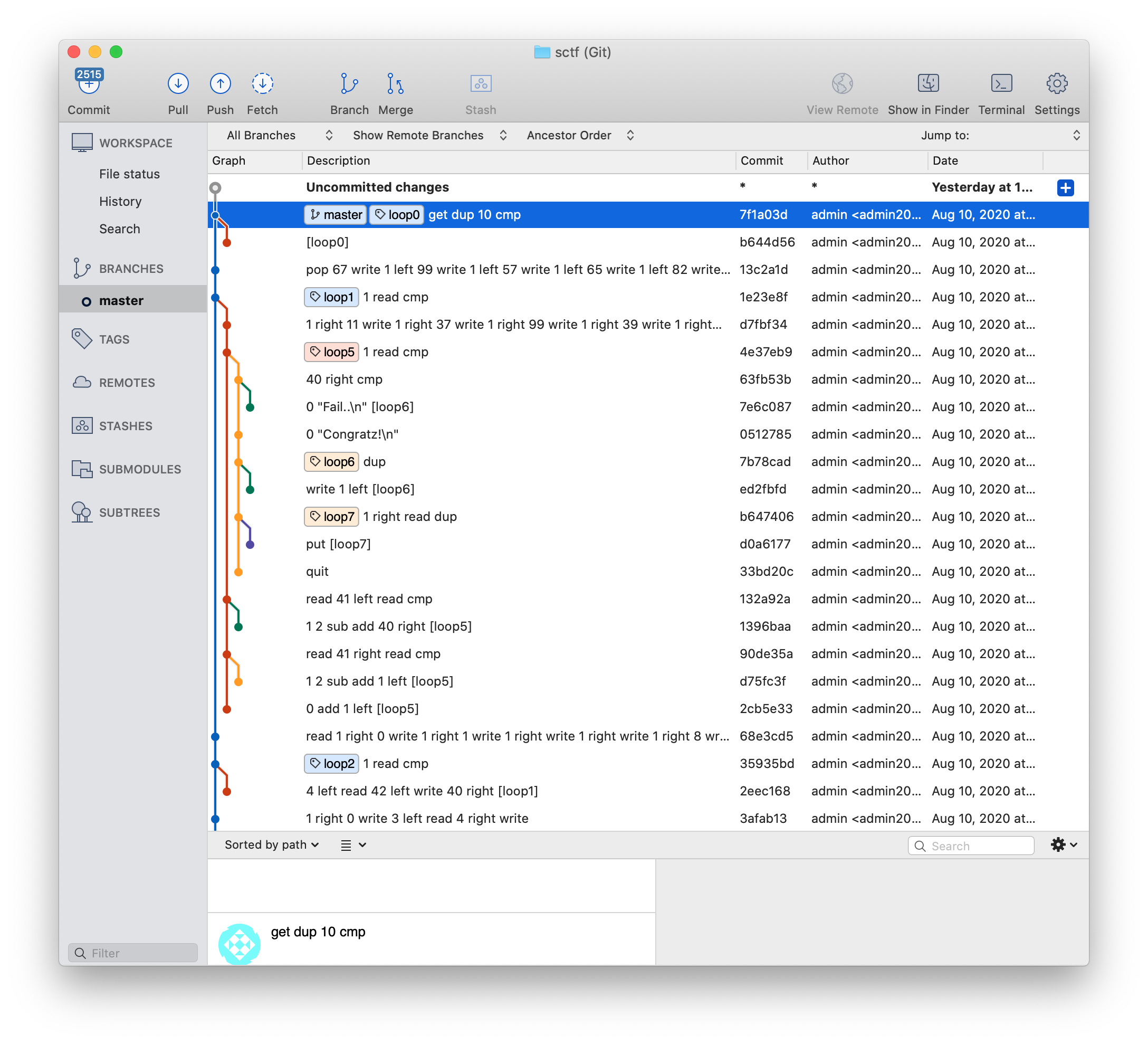
This seems to be some sort of program description. It looks like git branches represent actual control branches and git labels are being used as control flow labels.

Throughout the reversing process we need to learn what the operations are and how they work without being able to actually run the program. This requires a mix of guesswork, intution and reasoning.

Part 1: operations

Looking at the content of each git message, we see a mix of numbers and words. For example, one description is:

1 left read 3 left write 5 right read 4 left write 2 left read dup add write 3 right read 1 sub write [loop2]

To start making sense of this code, we can try to recognize familiar concepts and see if they apply. For instance dup reminds me of a stack-based language. Traditionally, dup is an instruction that means duplicate the topmost stack element. In such a language, operations are usually written in postfix notation. For example, (A * (B + C)) would be: B C add A mul.

Now we also see instructions like left, right, read and write that have Turing Machine connotations. Specifically, in a Turing Machine, there is linear memory tape that we can read and write to. However, instead of specifying a memory index, we move a “head” left and right to indicate the target position.

Note: read and write is also obviously used for input/output however in other git messages we see put and get which seem to be responsible for I/O.

If we use that intution to decompose the structure, we can guess the following basic instructions:

N           : push N to the stack (e.g. 0, 1, ...)
left        : pop N; idx -= N
right       : pop N; idx += N
read        : push mem[idx]
write       : pop V; mem[idx] = V
dup         : pop V; push V; push V
add         : pop B; pop A; push A+B
sub         : pop B; pop A; push A-B
get         : push getchar()
put         : pop V; putchar(V)
[lbl]       : goto lbl
quit        : quit
"abc"       : push characters a,b,c to the stack

There is still a cmp instruction that is a bit more elusive to figure out.

Part 2: control flow

Using the git tree, we see both conditional branching and unconditional goto type operations.

If we look at the start of the program we see the following operations:

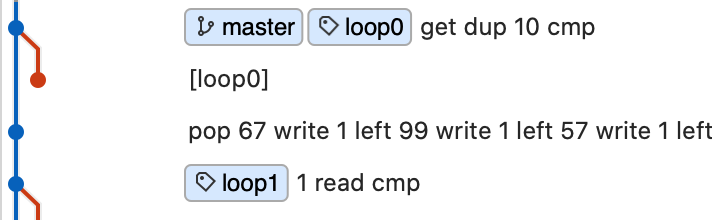
In pseudo-assembly, we have:

loop0:
    get dup 10 cmp

    new_branch: goto loop0
    same_branch: ...

Now we recognize the 10 as the ascii code for a newline (\n). In this case it would make sense for the program to keep reading input until it sees a newline, which indicates the user has pressed enter. So we can interpret this cmp as checking if the character we just read is equal to 10. If the condition is false, we take the new branch (in this case it just loops us back to loop0). If the condition is true, we stay on the same branch.

It turns out this is not exactly correct. cmp is actually performing pop B; pop A; push A >= B rather than pop B; pop A; push A == B. This will become obvious later.

Part 3: memory tape

One difficult aspect of a memory tape is all of our memory accesses are dependent on the current position of the tape head. That is, if we execute a left instruction before hitting the label loop2, we will edit different memory than if we had executed a right instruction. So we need a way to rationalize our memory usage and make sense of it.

Since this program was made by humans (as far as I can tell), we can take advantage of the fact that humans like simple structure and writing a program that consists of a lot of context-dependent memory access is farly difficult. A much more likely scenario is that a human designed a program with “variables” which allows for more flexibility in program design and these were either converted by hand or with a compiler to context-dependent locations on a memory tape.

So when we start reversing the actual control flow, it is useful to make the assumption that memory accesses will actually be fixed (at least within the local context). So within a section of code for example, a specific read instruction will always end up editing the same memory location even though we may take different paths to end up here.

Part 4: reversing the program

Input

The first part of the program just reads user input onto the stack:

loop0:
    get dup 10 cmp(loop0_t1,loop0_f1)
loop0_f1:
    goto loop0
loop0_t1:
    pop
    67 write 1 left 
    99 write 1 left 
    57 write 1 left 
    65 write 1 left 
    82 write 1 left 
    86 write 1 left 
    120 write 1 left 
    83 write 1 left 
    72 write 1 left 
    98 write 1 left 
    74 write 1 left 
    81 write 1 left 
    72 write 1 left 
    90 write 1 left 
    99 write 1 left 
    118 write 1 left 
    57 write 1 left 
    68 write 1 left 
    88 write 1 left 
    110 write 1 left 
    81 write 1 left 
    52 write 1 left 
    100 write 1 left 
    74 write 1 left 
    121 write 1 left 
    81 write 1 left 
    77 write 1 left 
    83 write 1 left 
    122 write 1 left 
    113 write 1 left 
    81 write 1 left 
    80 write 1 left 
    66 write 1 left 
    117 write 1 left 
    77 write 1 left 
    69 write 1 left 
    97 write 1 left 
    55 write 1 left 
    102 write 1 left 
    88 write 1 left 
    40 right                        #0
loop1(#N):
    ...

I’m using the notation cmp(true_label,false_label) when I transcribe.

In the right hand margins, I’ve added some annotations. #x indicates the memory tape position at a certain instruction.

loop1 is called with the memory index #0 (pointing to the first 67 we wrote). For simplicity, I’ve annotated variables below as if this #0 address is fixed. [...] expressions are showing stack variables.

loop1(#N):
    1 read                          [lN]
    cmp(loop1_t1,loop1_f1)          if (lN >= 1) #0
loop1_t1(#0):
    read                            [l0]
    1 right 0 write                 l1 = 0
    1 right 1 write                 l2 = 1
    1 right write                   l3 = l0
    1 right write                   l4 = <char>
    1 right 8 write                 l5 = 8
loop2(#5):
    ...

Here we see some local variables (lx) initialized. Also, we end up reading past the context of the local stack which means we read a character from the user input into l4.

loop2(#5):
    1 read cmp(loop2_t1,loop2_f1)   if (l5 >= 1)
loop2_f1(#5):
    4 left read                     [l1]
    42 left write                   l-41 = l1
    40 right                        #-1
    goto loop1                      #-1
loop2_t1(#5):
    1 right 0 write                 l6 = 0
    3 left read                     [l3]
    4 right write                   l7 = l3
loop3(#7):
    ...

We see that the end of this loop will return to loop1 with a memory index of N-1. So we are essentially iterating backwards over those characters from earlier. We also store the result of something to l-41 which is just before the section of 40 chars.

loop3(#7):
    2 read cmp(loop3_t1,loop3_f1)   if (l7 >= 2) #7
loop3_f1(#7):
    1 right 0 write                 l8 = 0
    4 left read                     [l4]
    5 right write                   l9 = l4
loop4(#9):
    2 read cmp(loop4_t1,loop4_f1)   if (l9 >= 2) #9
loop4_f1(#9):
    read                            [l9]
    2 left read                     [l9, l7]
    cmp(loop4_t2,loop4_f2)          if (l9 >= l7) #7
loop4_f2(#7):
goto1(#7):
    5 left read                     [l2]
    1 left read                     [l2, l1]
    add write                       l1 = l1+l2
    6 right                         #7
goto2(#7):
    1 left read                     [l6]
    3 left write                    l3 = l6
    5 right read                    [l8]
    4 left write                    l4 = l8
    2 left read                     [l2]
    dup add write                   l2 = l2 * 2
    3 right read                    [l5]
    1 sub write                     l5 = l5 - 1
    goto loop2
loop4_t2(#7):
    read                            [l7]
    2 right read                    [l7, l9]
    cmp(loop4_t3,loop4_f3)          if (l7 <= l9)   #9
loop4_f3(#9):
    2 left
    goto goto1                      #7
loop4_t3(#9):
    2 left
    goto goto2                      #7
loop4_t1(#9):
    1 left 1 read add write         l8 = l8 + 1
    1 right read 2 sub write        l9 = l9 - 2
    goto loop4
loop3_t1(#7):
    1 left 1 read add write         l6 = l6 + 1
    1 right read 2 sub write        l7 = l7 - 2
    goto loop3

The rest of this section does some more arithmetic and maintains locally consistent memory accesses. For example, notice that in loop4_f3 and loop4_t3 we enter with a memory index of #9 and there is a 2 left before the goto so that we adjust to index #7 before hitting goto1 and goto2.

It turns out this section ends up being called once for each character in the bytestream and the value we store in l-41 is logically interpreted as the return value. So we can translate this section directly to python:

def loop1(v, c):
    '''
    v = char from byte sequence
    c = user input char
    '''
    l1 = 0
    l2 = 1
    l3 = v
    l4 = c
    l5 = 8

    # loop2
    while l5 >= 1:
        l6 = 0
        l7 = l3

        # loop3
        while (l7 >= 2):
            l6 += 1
            l7 -= 2
    
        l8 = 0
        l9 = l4

        # loop4
        while (l9 >= 2):
            l8 += 1
            l9 -= 2
        
        if l9 != l7:
            # goto1
            l1 += l2

        # goto2
        l3 = l6
        l4 = l8
        l2 *= 2
        l5 -= 1

    return l1

After we have iterated over all 40 bytes, we will hit a null byte and reach loop1_f1:

loop1_f1(#0):
    1 right 11 write 
    1 right 37 write 
    1 right 99 write 
    1 right 39 write 
    1 right 62 write 
    1 right 126 write 
    1 right 64 write 
    1 right 114 write 
    1 right 103 write 
    1 right 98 write 
    1 right 3 write 
    1 right 75 write 
    1 right 16 write 
    1 right 18 write 
    1 right 96 write 
    1 right 74 write 
    1 right 124 write 
    1 right 85 write 
    1 right 3 write 
    1 right 14 write 
    1 right 45 write 
    1 right 42 write 
    1 right 29 write 
    1 right 105 write 
    1 right 65 write 
    1 right 83 write 
    1 right 5 write 
    1 right 121 write 
    1 right 100 write 
    1 right 21 write 
    1 right 47 write 
    1 right 124 write 
    1 right 101 write 
    1 right 73 write 
    1 right 21 write 
    1 right 13 write 
    1 right 25 write 
    1 right 9 write 
    1 right 17 write 
    1 right 62 write                #41
    0                               [c=0]
loop5(#N):
    ...

Here we store a size 40 byte sequence (to the right this time) and enter loop5. Before starting though, we push a 0 which will act as an “incorrect char” counter.

    0                               [c=0]
loop5(#N):
    1 read                          [c, lN]
    cmp(loop5_t1,loop5_f1)          if (lN >= 1) #N
loop5_t1(#N):
    read                            [c, lN]
    41 left read                    [c, lN, lN-41]
    cmp(loop5_t3,loop5_f3)          if (lN >= lN-41) # N-41
loop5_f3(#N-41):
    1 2 sub                         [c, -1]
    add                             [c-1]
    40 right                        #N-1
    goto loop5(#N-1)
loop5_t3(#N-41):
    read                            [c, N-41]
    41 right read                   [c, N-41, N]
    cmp(loop5_t4,loop5_f4)          if (lN-41 >= lN) #N
loop5_f4(#N):
    1 2 sub                         [c, -1]
    add                             [c-1]
    1 left                          #N-1
    goto loop5(#N-1)
loop5_t4(#N):
    0 add
    1 left                          #N-1
    goto loop5(#N-1)
loop5_f1(#N):
    ...

Each iteration we compare lN to lN-41 (value written from the previous section) and check for equality. If these values are the same, we simply iterate to loop5(#N-1). If they are different, we decrement the stack value c before looping to loop5(#N-1).

Once we have finished iterating over all 40 chars, we hit loop5_f1:

loop5_f1(#N):
    40 right                        #N+40
    cmp(loop5_t2,loop5_f2)          if (c >= 0) #N+40
loop5_f2:
    0 "Fail..\n"
    goto loop6
loop5_t2:
    0 "Congratz!\n"
loop6:
    dup 
    0 cmp(loop6_t1,loop6_f1)
loop6_f1:
    write
    1 left
    goto loop6
loop6_t1:
loop7:
    1 right
    read
    dup 0 cmp(loop7_t1,loop7_f1)
loop7_t1:
    quit
loop7_f1:
    goto loop7

If c >= 0 (i.e. no incorrect chars), it prints out Congratz! otherwise it prints Fail...

Part 5: solution

Now that we understand the control flow, we can write a solver. Essentially we need to find a valid character for each byte in the original byte stream so that the saved value (in lN-41) equals the second byte stream. This is a simple size 256 brute force per character. Using our python implementation, we can do the following:

orig = [88, 102, 55, 97, 69, 77, 117, 66, 80, 81, 113, 122, 83, 77, 81, 121, 74, 100, 52, 81, 110, 88, 68, 57, 118, 99, 90, 72, 81, 74, 98, 72, 83, 120, 86, 82, 65, 57, 99, 67]
target = [11, 37, 99, 39, 62, 126, 64, 114, 103, 98, 3, 75, 16, 18, 96, 74, 124, 85, 3, 14, 45, 42, 29, 105, 65, 83, 5, 121, 100, 21, 47, 124, 101, 73, 21, 13, 25, 9, 17, 62]

flag = ''

for i in range(40):
    for c in range(128):
        val = loop1(orig[i], c)
        if val == target[i]:
            flag += chr(c)
            break
            
print(flag)

SCTF{35073r1C_13617_CrYP70_15_M461C_X0r}

Part 6: easier solution

As it turns out, this fancy math is just computing xor and it seems like many people saw these byte sequences and just tried:

orig = [88, 102, 55, 97, 69, 77, 117, 66, 80, 81, 113, 122, 83, 77, 81, 121, 74, 100, 52, 81, 110, 88, 68, 57, 118, 99, 90, 72, 81, 74, 98, 72, 83, 120, 86, 82, 65, 57, 99, 67]
target = [11, 37, 99, 39, 62, 126, 64, 114, 103, 98, 3, 75, 16, 18, 96, 74, 124, 85, 3, 14, 45, 42, 29, 105, 65, 83, 5, 121, 100, 21, 47, 124, 101, 73, 21, 13, 25, 9, 17, 62]

flag = ''.join([chr(x^y) for x,y in zip(orig,target)])
print(flag)

SCTF{35073r1C_13617_CrYP70_15_M461C_X0r}

Conclusion

I really enjoyed this problem despite not finding the quick solution. There is a real joy to incrementally uncovering parts of a program until all the puzzle pieces start to fit together. I am a bit disappointed that there was such an easy solution to the problem, usually it’s much cooler to embed a deeper problem behind a layer of reversable obfuscation. In this case, I think it was too easy to get a surface level understanding of the problem and guess the solution.