TetCTF 2022 - crackme pls (964 pt / 7 solves)
Control flow de-obfuscation.
January 2, 2022
rev
crackme pls (964 pt / 7 solves)
Description:
Just a simple crackme, but we spiced it up a little bit.
Files:
Overview
Happy New Year!
This was a fun reversing challenge and an interesting exploration in using cool hacker tools :tm: to perform some automatic control-flow recovery.
The problem primarily consisted of two parts:
- figuring out how to de-obfuscate the control flow
- reversing child/parent PTRACE shenanigans
In this writeup, I’ll primarily focus on the first part because I found it really interesting and I think some of these techniques could be useful for other problems.
The problem
Opening up main, we are greeted with a dead end:
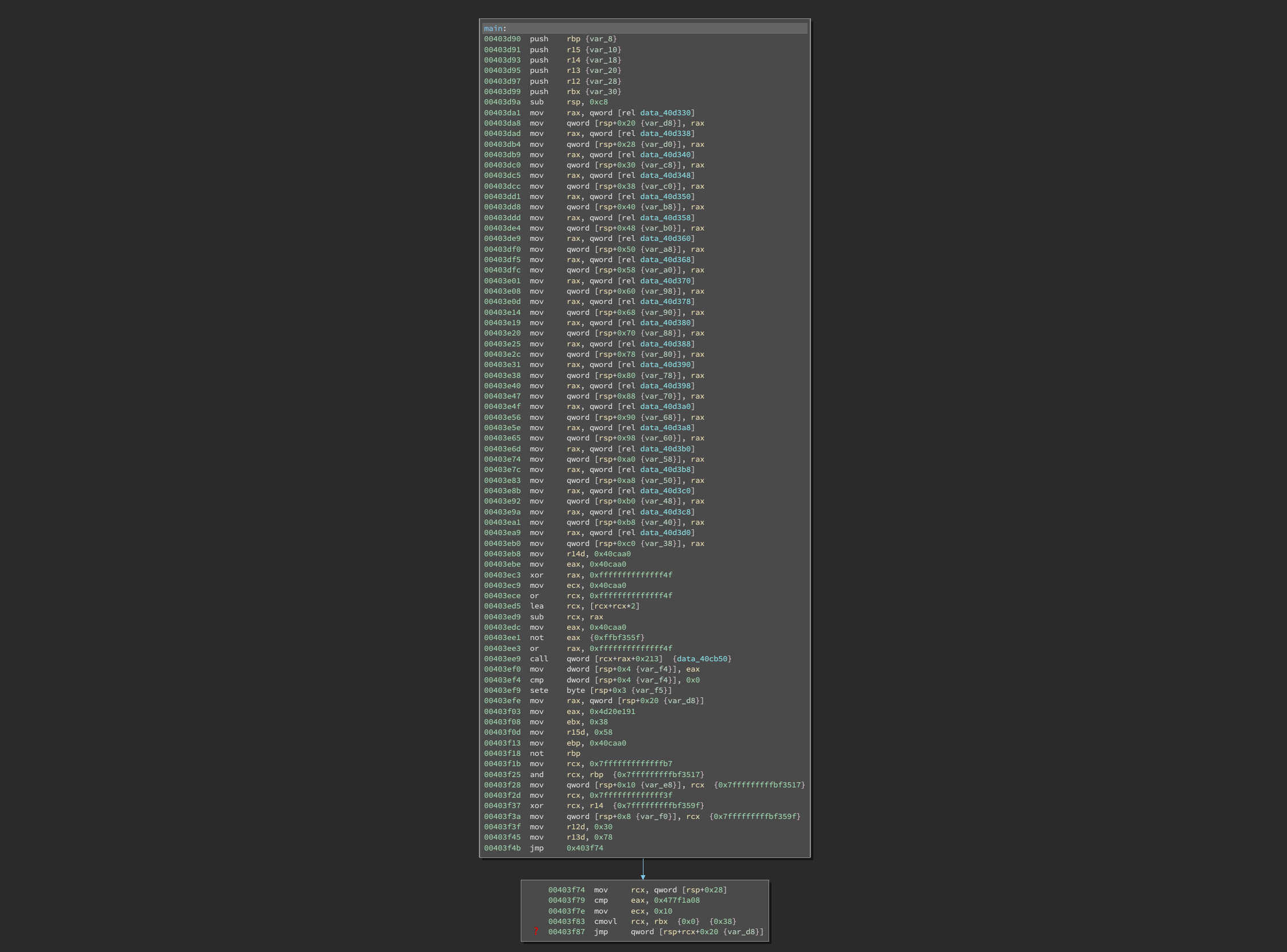
Binary Ninja remorsefully displays a ❓ indicating that it was unable to figure out the indirect control flow.
Scanning the function, we see several features:
- a function table is set up at stack offset
+0x20 - the indirect jump jumps into this function table at one of two possible offsets
403f74 mov rcx, qword [rsp+0x28]
403f79 cmp eax, 0x477f1a08
403f7e mov ecx, 0x10
403f83 cmovl rcx, rbx {0x0} {0x38}
403f87 jmp qword [rsp+rcx+0x20 {var_d8}]
We can translate this by hand into:
if (eax < 0x477f1a08) goto table[7]; // +0x38
else goto table[2]; // +0x10
And we can lookup those table values to get:
table[2] == 0x403fd0
table[7] == 0x403f8b
Now to convince Binary Ninja of these possible jumps, we need to break out some Python:
# get main func
func = bv.get_function_at(0x403d90)
# tell binja this instruction will jump places
func.set_user_indirect_branches(
0x403f87,
[[bv.arch, 0x403fd0], [bv.arch, 0x403f8b]]
)
And voila:
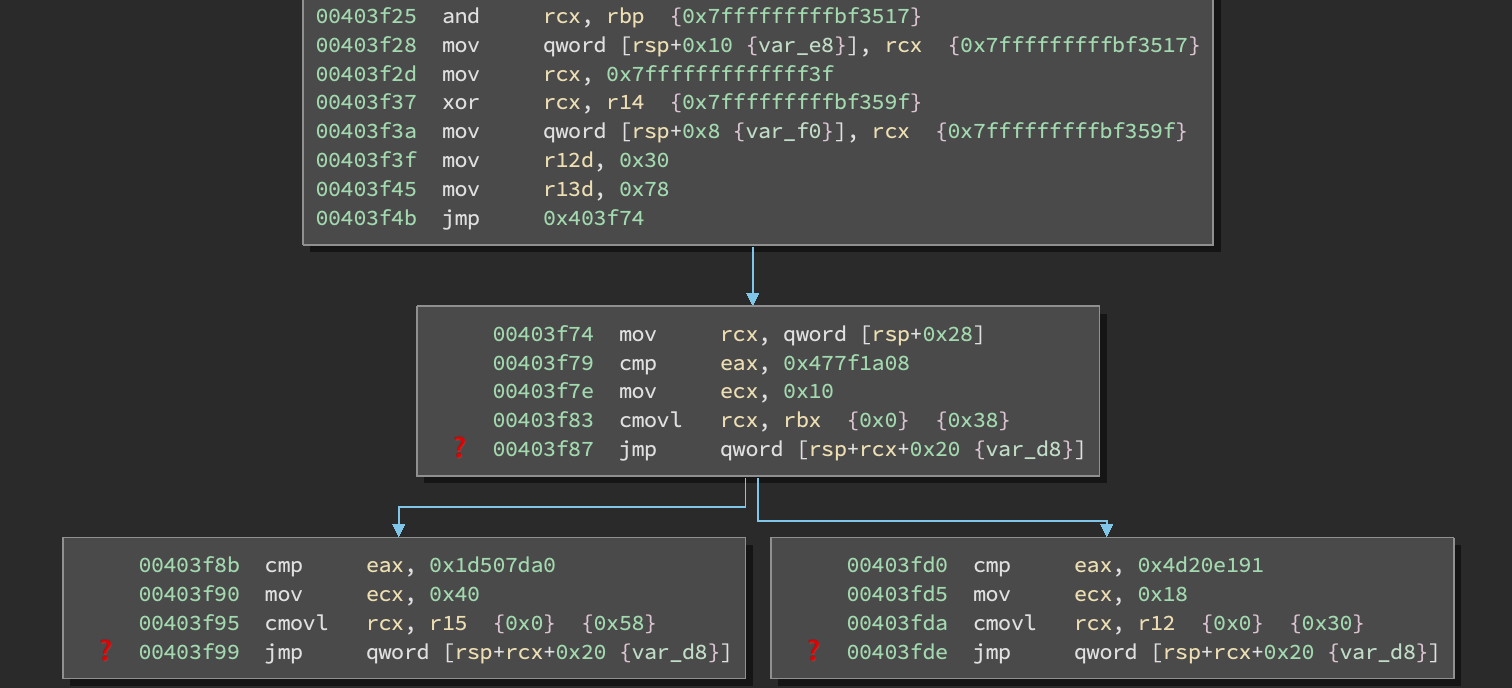
Hmm, same problem! Repeat:
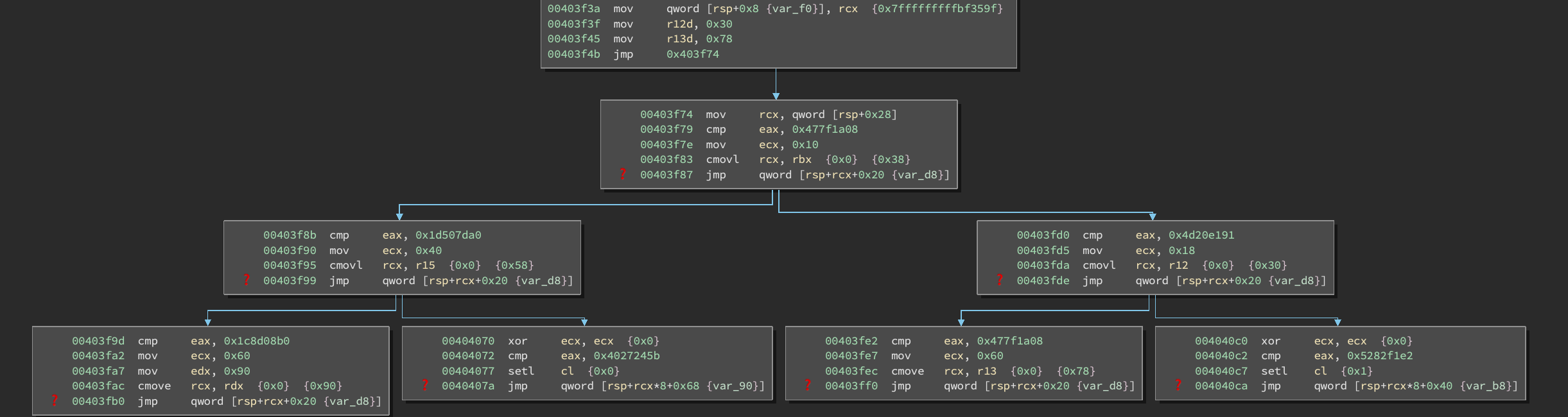
And repeat:
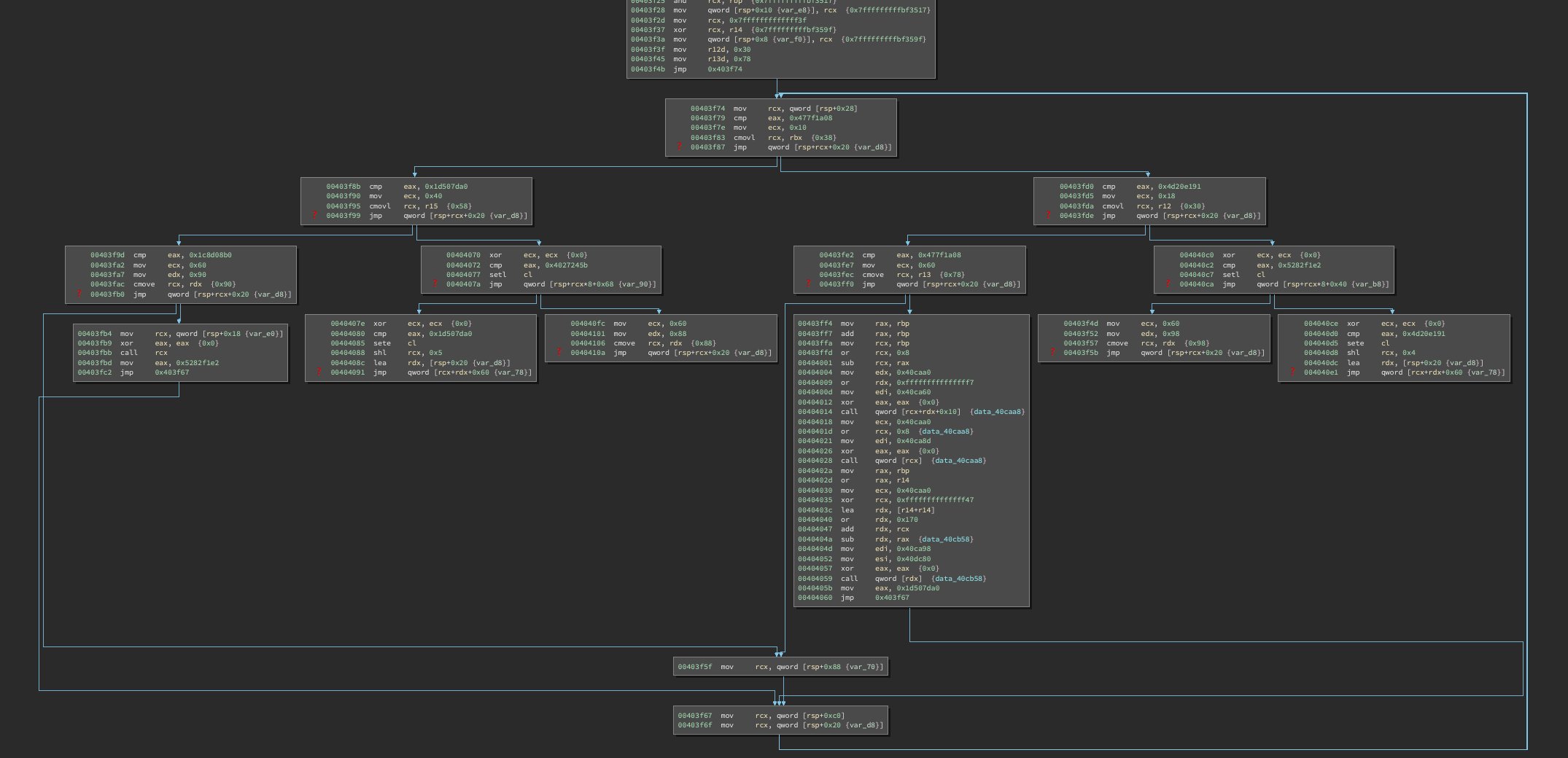
And repeat:
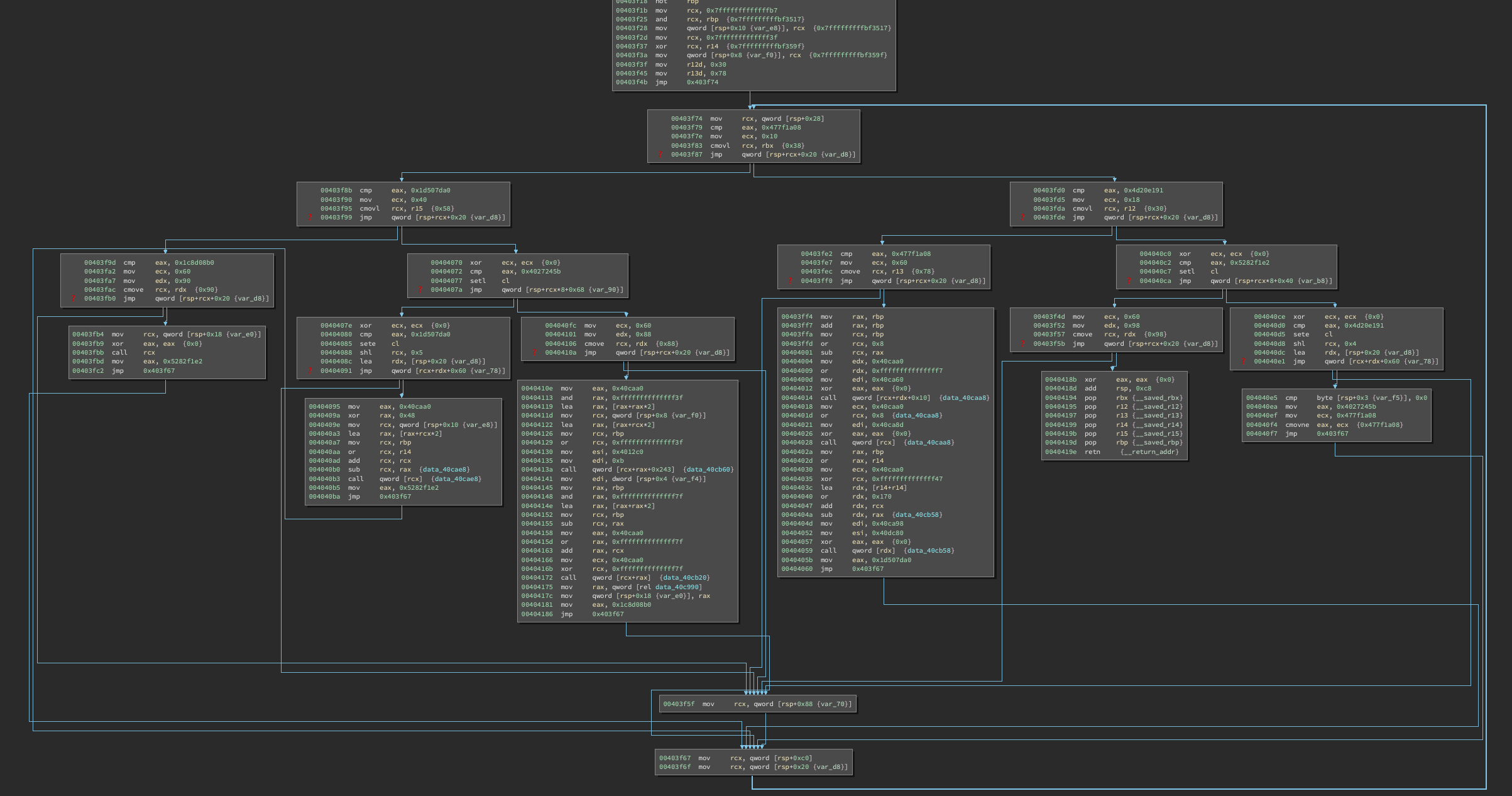
The structure of control flow becomes more apparent. Essentially, we have something like the following:
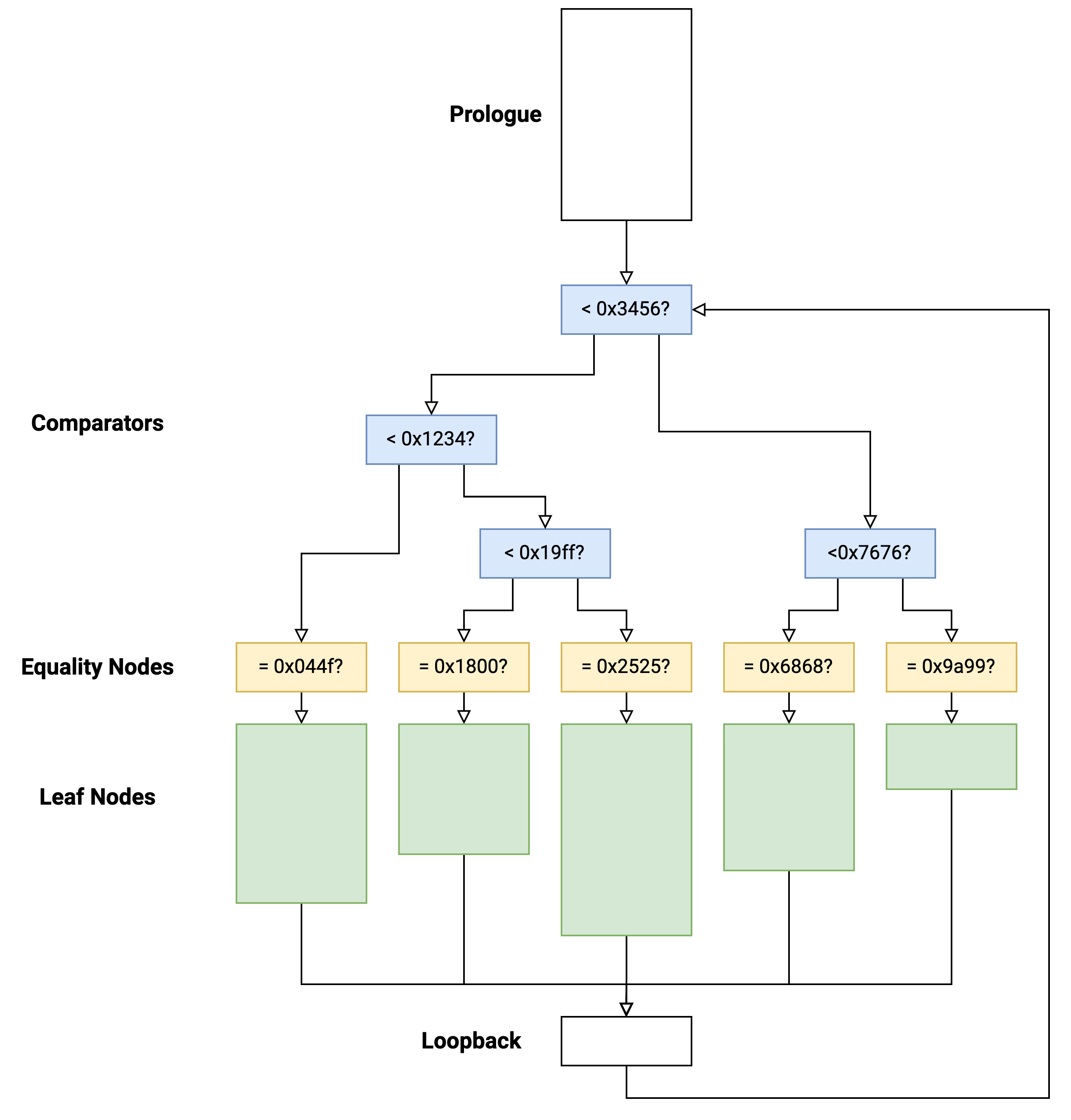
Each function consists of:
- a prologue (top white block)
- comparator nodes (blue)
- equality nodes (yellow)
- leaf nodes (green)
- loopback node (white bottom)
Control flow operates based on a key value (32-bit value, typically stored in a single register).
The comparators are arranged in a binary tree to route execution to the target leaf function. If the key value matches exactly with an equality node, execution enters a leaf function which contains “real” code.
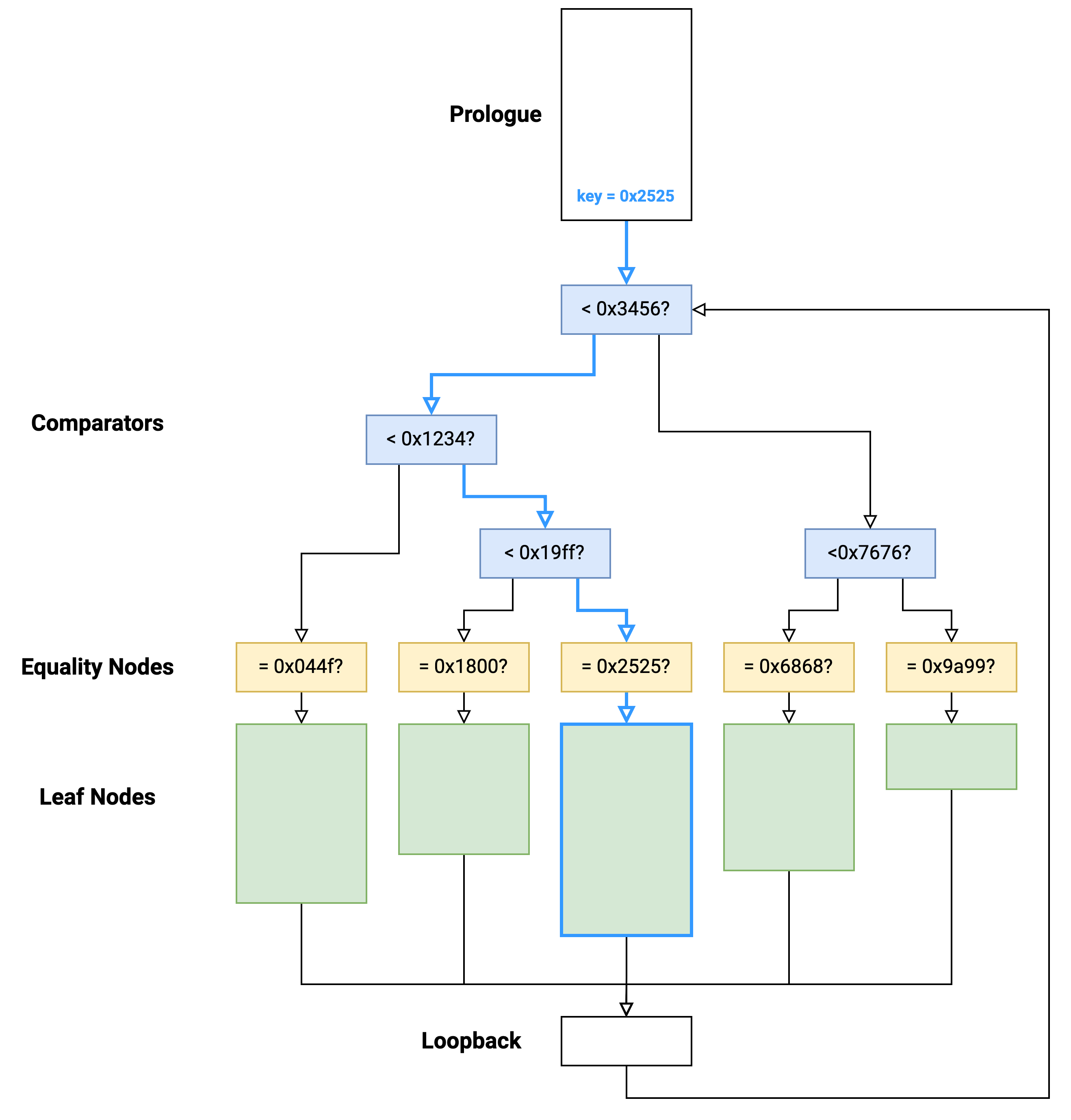
At the end of a leaf function, the key is updated with a new value and execution transfers back to the start of the comparator tree:
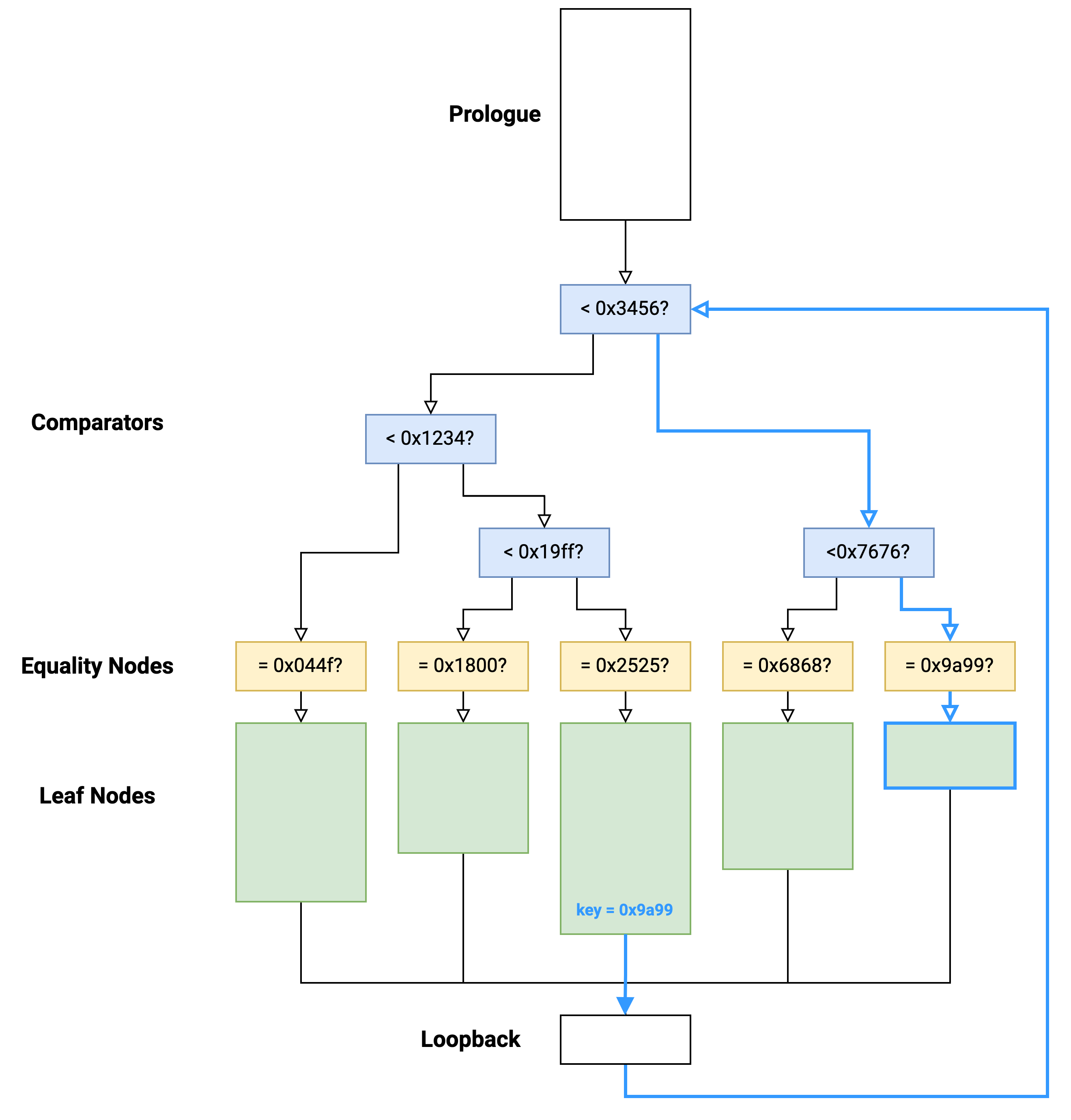
Effectively, this is just an indirect jump from one leaf node to another.
Some leaf nodes conditionally set the key value, which means the target leaf may be one of two choices:
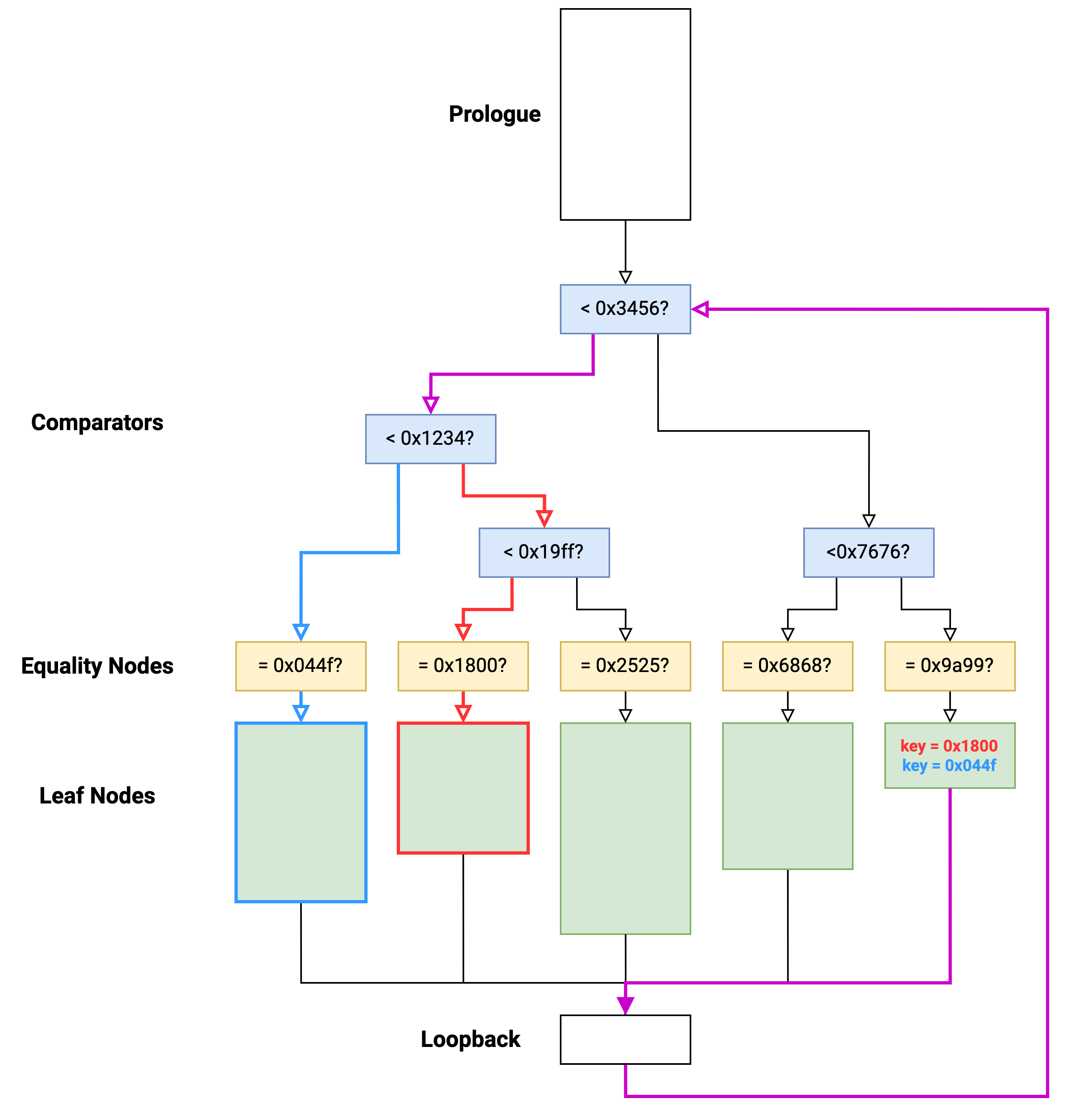
In order to understand the program logic, we really want to visualize the control flow between leaf nodes:
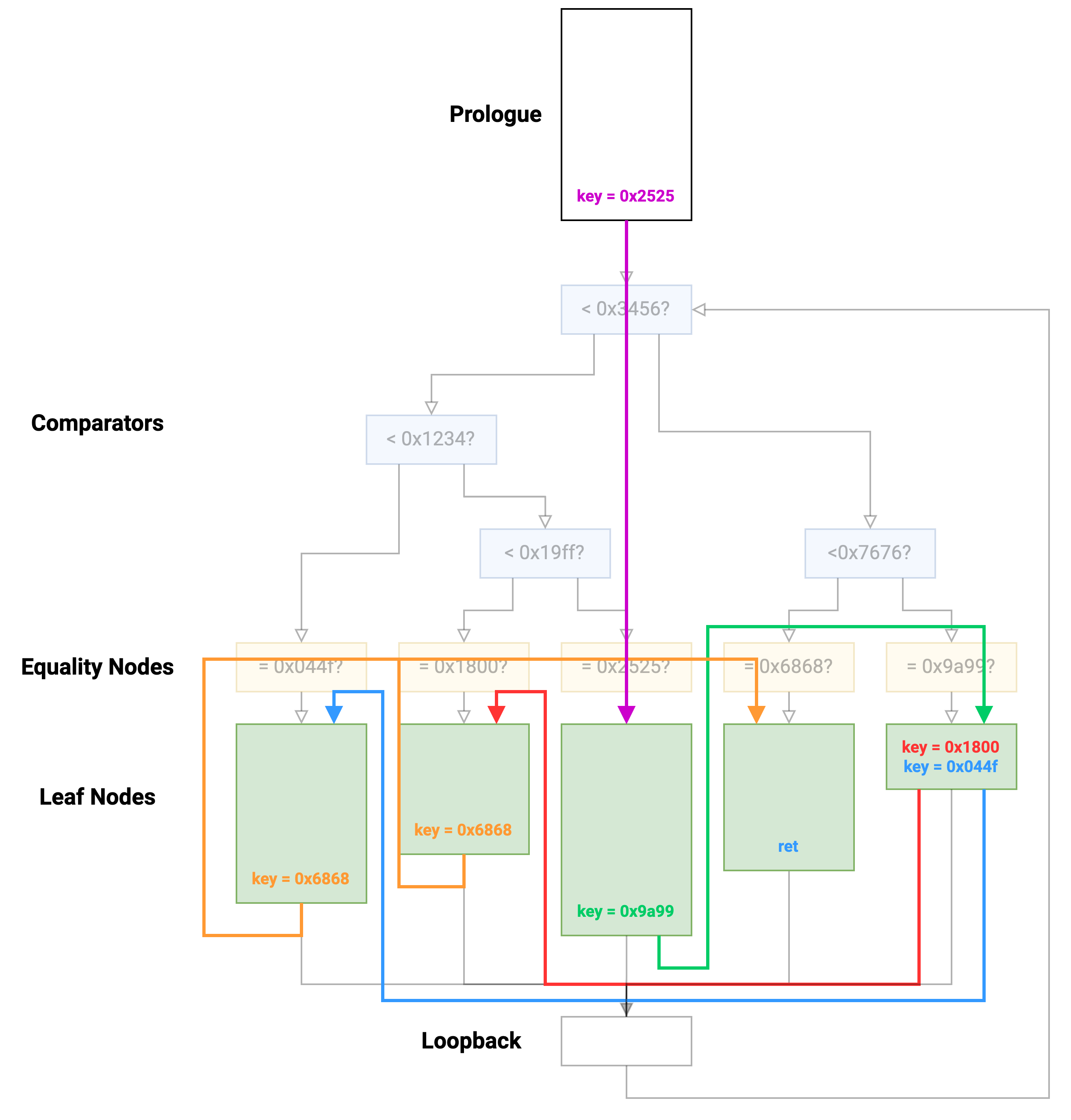
This will also look much simpler if we remove all non-leaf nodes:
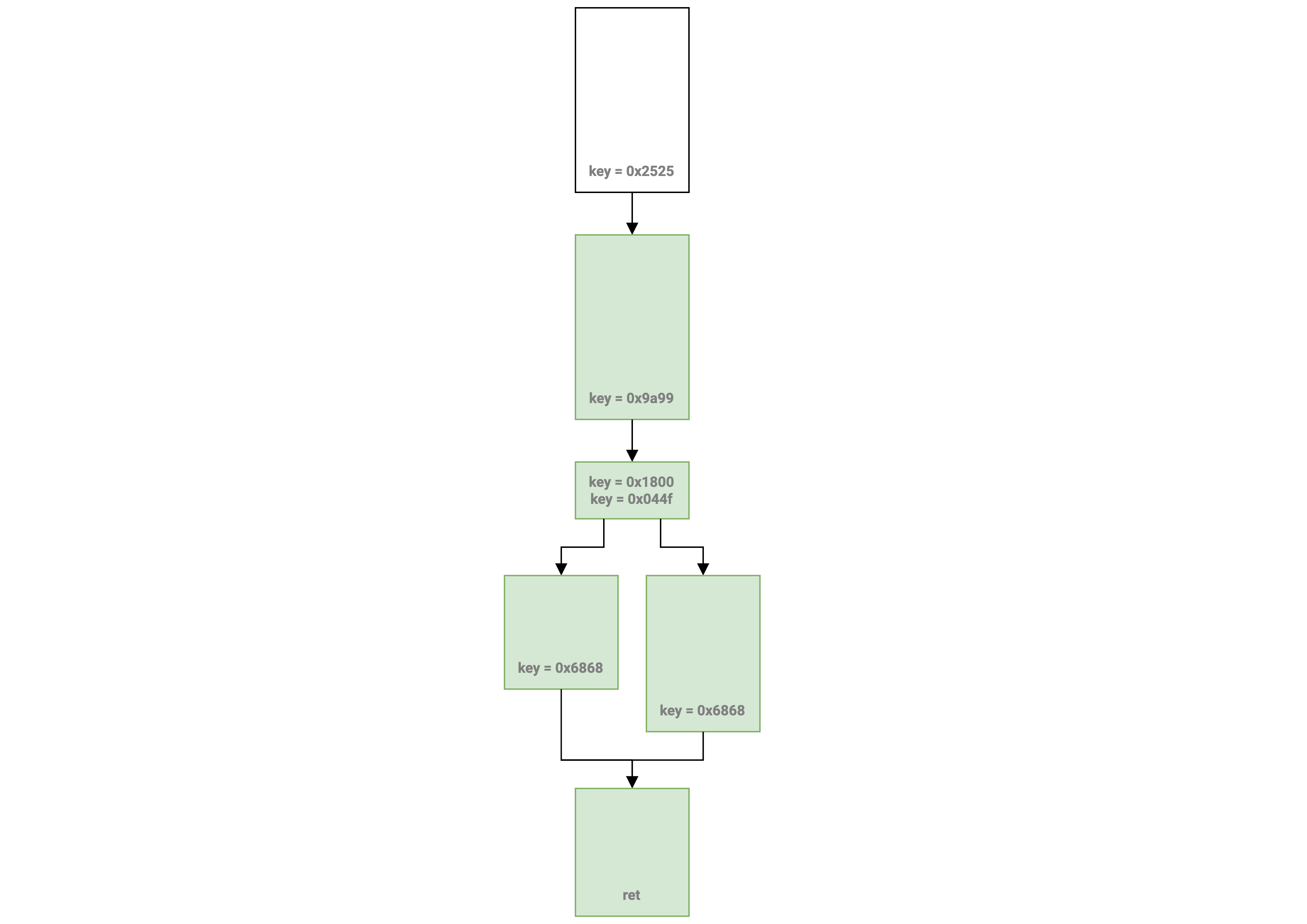
And now we’ve recovered close to the original control flow!
Automation
Now the question is: How can we do this automatically?
For a given function, we need to solve the following subproblems:
- dump the function table from the prologue
- figure out which blocks are leaf nodes
- find the key value corresponding to each leaf node
- find the target keys from each leaf node (where will this leaf jump next?)
- rewire the unconditional jumps to get a nice view
1. Function Table
After looking at several functions, we can see that the function table setup code is always the first thing that happens (right after stack frame setup):
00403d90 push rbp {__saved_rbp}
00403d91 push r15 {__saved_r15}
00403d93 push r14 {__saved_r14}
00403d95 push r13 {__saved_r13}
00403d97 push r12 {__saved_r12}
00403d99 push rbx {__saved_rbx}
00403d9a sub rsp, 0xc8
00403da1 mov rax, qword [rel data_40d330] ; first entry
00403da8 mov qword [rsp+0x20 {var_d8}], rax
00403dad mov rax, qword [rel data_40d338] ; second entry
00403db4 mov qword [rsp+0x28 {var_d0}], rax
We can use Capstone to disassemble the first few instructions and find the first mov instruction:
import capstone
md = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
code = open('./crackme-pls.bin', 'rb').read()
BASE = 0x400000
def find_table_base(function_addr):
instructions = md.disasm(code[function_addr-BASE:], function_addr)
for i in range(50):
t = next(instructions)
if (t.mnemonic == 'mov' and
t.op_str.startswith('rax, qword ptr [rip')):
# e.g.:
# mov rax, qword ptr [rip + 0x1234]
off = t.op_str.split('+ ')[1].split(']')[0]
off = int(off, 16)
table_base = (t.address + t.size + off)
return table_base
return None
Luckily, the compiler generated zero-terminated arrays, so we can happily read pointers from table_base until we hit a zero without doing any more analysis.
2 & 3. Key to leaf node mapping
I spent a while searching for some easy-to-parse pattern with the comparator and equality nodes. However, the compiler generated a bunch of weird optimizations that made pattern-hunting fairly difficult. For instance, these were some differences between functions and nodes:
- different stack offsets
- different register for key value
- different indirect jmp formats (setl + shift, setl no shift, cmp, sete…)
I decided it would be easier to use symbolic execution and I chose Angr because I was already fairly familiar with it.
My plan was the following:
- Execute from the function start until the first comparator node (to prepare the function table context).
- Replace the key value register with a symbolic variable.
- Pathfind to every function address in the function table.
- Upon finding a path to the function, see if the symbolic key variable has exactly one solution. If it does, this is a leaf node and we know the key value, if it doesn’t this is not a leaf node (underconstrained).
Early on, I ran into a slight hiccup with the fact that several function prologues execute call instructions to things like fork or signal which really confuses symbolic execution. However, we don’t actually care about the return value of these functions since we only need to initialize the function table, so to bypass the calls, I manually single-stepped with Angr and then used Capstone to check if the next instruction is a call. For each call, I manually increment rip and remove any constraints on rax (the unknown return value):
import angr
import claripy
import capstone
md = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
code = open('./crackme-pls.bin', 'rb').read()
BASE = 0x400000
p = angr.Project('./crackme-pls.bin')
def trace_function(fn_addr, first_comparator, table, code, keyreg='eax'):
# Prepare the initial state.
state = p.factory.call_state(addr=fn_addr)
simgr = p.factory.simulation_manager(state)
# Single step until we hit the first comparator.
while True:
simgr.step(num_inst=1)
curr = simgr.active[0].addr
instr = next(md.disasm(code[curr - BASE:], curr))
# If this is a call, skip it.
if instr.mnemonic == 'call':
simgr.active[0].regs.rip += instr.size
# Unconstrain rax.
simgr.active[0].regs.rax = claripy.BVS('fake', 64)
if curr == first_comparator:
break
# Step past first instruction (so we can use it in avoid).
simgr.step(num_inst=1)
# Clear keyreg
key_bv = claripy.BVS('key', 32)
setattr(simgr.active[0].regs, keyreg, key_bv)
# function -> key
lookup = {}
for fn in table:
fsim = simgr.copy(deep=True)
# Set avoid=init to prevent looping around.
fsim.explore(find=fn, avoid=init)
if len(fsim.found) == 1:
f = fsim.found[0]
unique = False
try:
# Fails if there is just one solution.
f.solver.eval_atleast(key_bv, 2)
except:
unique = True
if unique:
key = f.solver.eval(key_bv)
lookup[fn] = key
return lookup
4. Finding where each leaf node goes next
For this task, I took the super lazy approach of simply grepping for other leaf node keys in the disassembly of each leaf block.
For leaf nodes with just one target, this works perfectly. However, for leaf nodes that conditionally branch, we lose the information about which node corresponds to which condition (and in general this is a hard problem to figure out).
If you have any ideas, let me know!
import binaryninja
from typings import List, Tuple, Dict
def find_fn_xrefs(block: binaryninja.BasicBlock, keys: List[int]) -> List[int]:
'''Returns which keys (if any) are in the disassembly for a given block.'''
txt = ''
for line in block.disassembly_text:
txt += ' '.join([tok.text for tok in line.tokens]) + '\n'
xrefs = []
for key in keys:
if hex(key) in txt:
xrefs.append(key)
return xrefs
def get_mappings(lookup: Dict[int, int], fn_addr: int, fkey: int) -> List[Tuple[int, List[int]]]:
'''
Given a lookup table of fn/key values, returns all the leaf
to leaf mappings.
'''
trace = []
# key -> fn
rev_lookup = {lookup[k]: k for k in lookup}
bv = binaryninja.BinaryViewType['ELF'].get_view_of_file(
'./crackme-pls.bin')
for k in lookup:
# Mark each node as a function to generate basic block info.
bv.add_function(k)
bv.update_analysis_and_wait()
for k in lookup:
blk = bv.get_basic_blocks_at(k)[0]
xrefs = find_fn_xrefs(blk, [lookup[k] for k in lookup])
targets = [rev_lookup[x] for x in xrefs]
trace.append((k, targets))
start_block = bv.get_basic_blocks_at(fn_addr)[0]
loop_block = start_block.outgoing_edges[0].target
trace.append((loop_block.start, [rev_lookup[fkey]]))
return trace
5. Rewiring with Binary Ninja
Now that we have this information about which leaf nodes jump to which other leaf nodes, we need to tell Binary Ninja.
We can use the same API as before to do so, e.g. func.set_user_indirect_branches.
There is one main problem that I ran into during experiments: If you mark an indirect branch on a instruction that isn’t an indirect branch (e.g. a normal branch like a jmp 0xabc) you won’t see this edge in the CFG. To get around this, I patched the end of each leaf node with jmp rax, effectively forcing every jump to be an indirect jump so that I could later override the target address with whatever I computed with Angr.
If you know a better workaround, please let me know!
Another smaller issue is that the Angr traces actually give us the mapping between the start address of each block and not the address of each jmp instruction. So we need to do a bit of extra work to find the last instruction in each block:
def set_targets(bv: binaryninja.BinaryView, src: int, targets: List[int]):
blocks = bv.get_basic_blocks_at(src)
if len(blocks) == 0:
return
blk = blocks[0]
func = blk.function
# Find the last instruction (the jmp).
_,addr = blk.get_instruction_containing_address(
blk.start + blk.length - 1)
# Apply indirect branches.
# (only works if the instruction at addr is an indirect jump)
func.set_user_indirect_branches(addr, [[bv.arch, x] for x in targets])
Results
Applying this technique to the binary, we get a much cleaner main function:

Binary Ninja can even generate some readable decompilation:
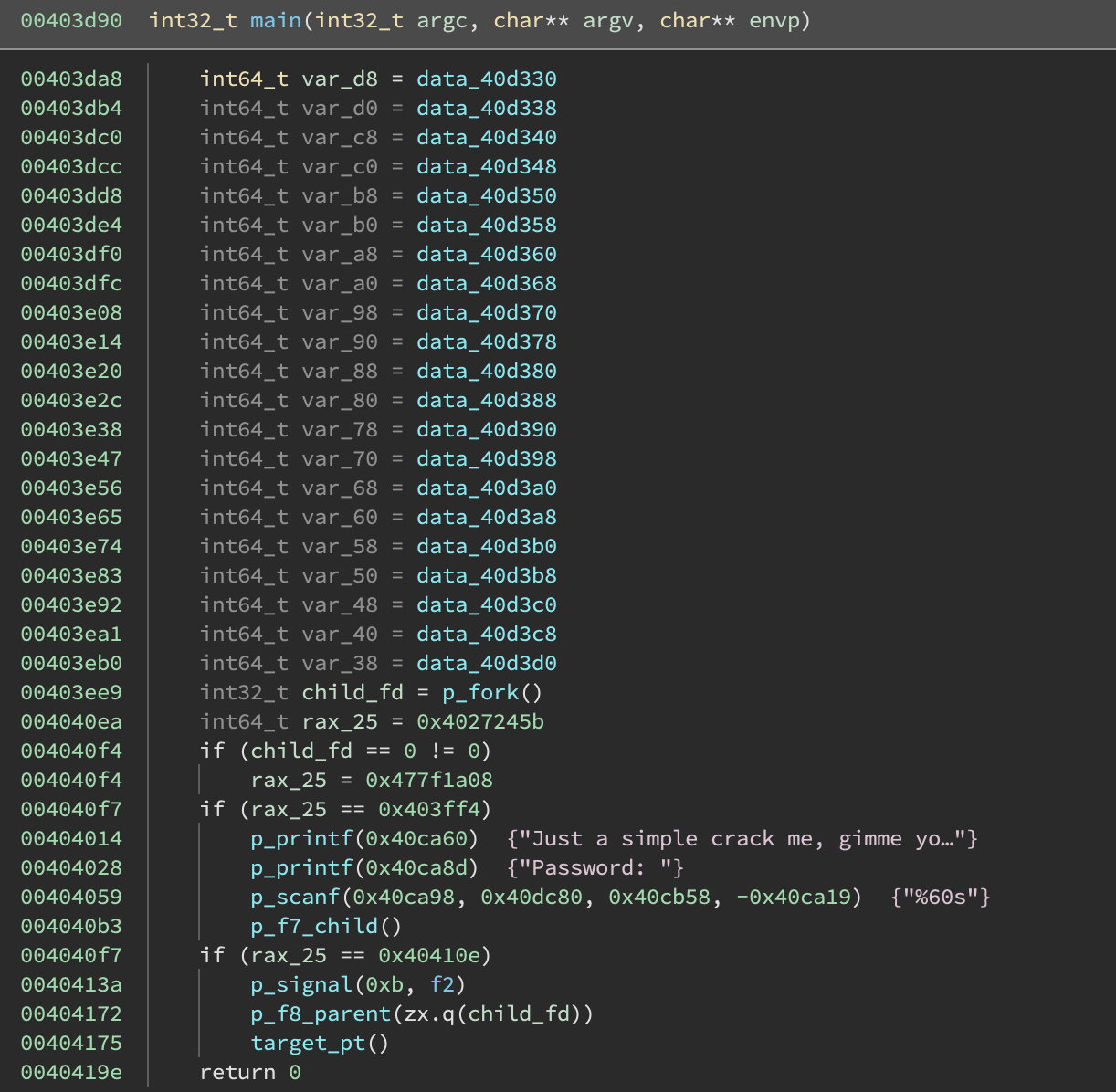
The main remaining issue is that conditionals don’t show up properly (because we don’t include any conditional information from the angr trace). But in this case, we can see that the result of fork() is dictating which branch will be taken.
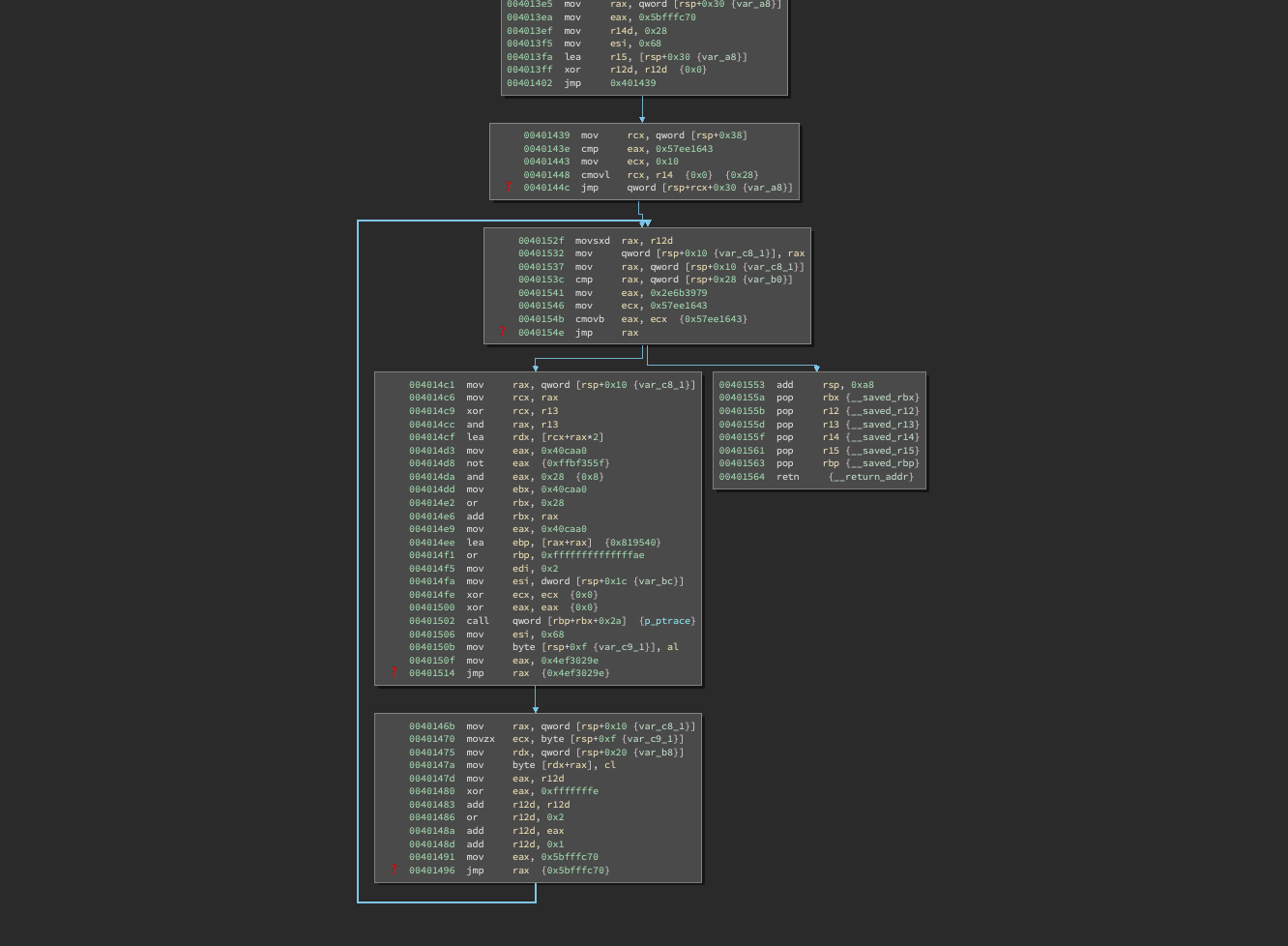
As another example, here’s a function that copies bytes from a child process using ptrace and we can see a very clear for-loop structure in the recovered CFG:
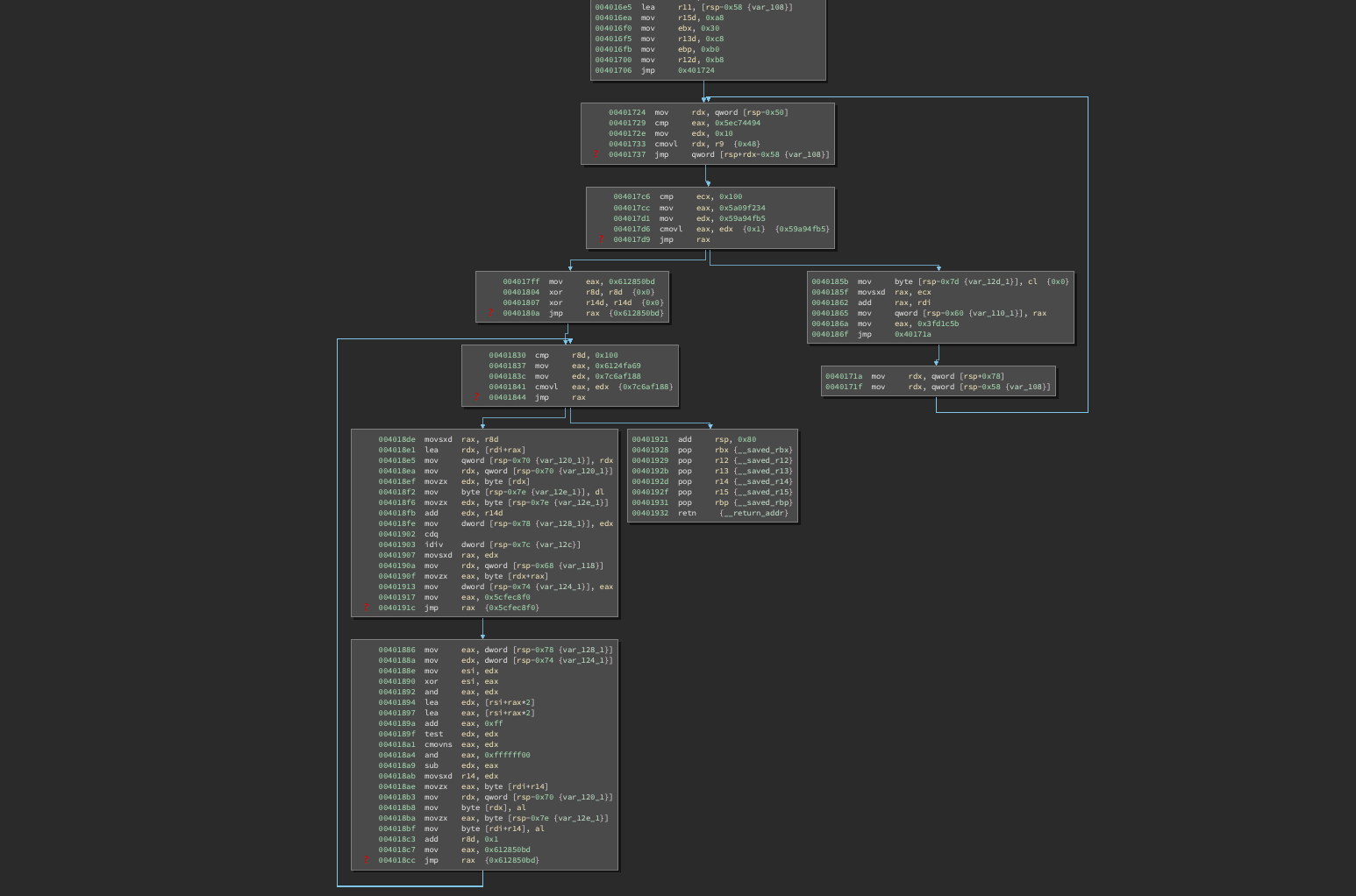
In another crypto-related function, the recovered control flow has two for-loops, one after the other:
See also
I’ll defer to these other writeups for the specifics of the actual problem:
- (mochi753, team: Wanna.One) https://hackmd.io/@mochinishimiya/SJ4JpI1ht#RE-crackme-pls