GoogleCTF 2022 - eldar (333 pt / 14 solves)
Lifting a weird ELF relocation machine.
July 3, 2022
rev
esoteric
Eldar
Description:
We found this app on a recent Ubuntu system, but the serial is missing from
serial.c. Can you figure out a valid serial?
Just put it into
serial.cand run the app withmake && make run.
Thanks!
Note: you don’t have to put anything else other than the serial into
serial.cto solve the challenge.
Challenge code is available here: https://github.com/google/google-ctf/tree/master/2022/rev-eldar
Prologue
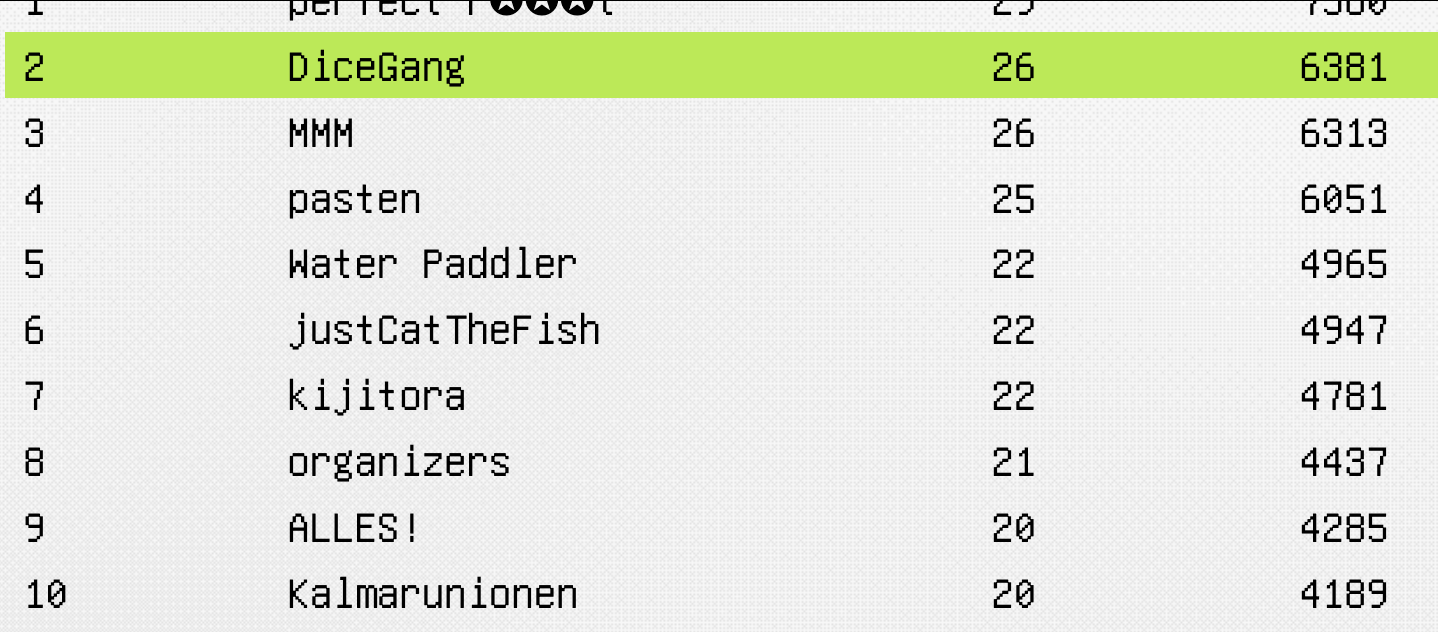
I played GoogleCTF 2022 with DiceGang and we got second place! I spent close to 12 hours on this challenge and tried a lot of things that ended up not working including:
- throwing everything into z3
- emulate in python
- translate to C and emulate faster
Eventually the approach that ended up working was disassembling everything and applying 11 lifter passes to reduce the number of instructions from 100k+ to ~1500. (and then throwing select parts into z3)
My lifting implementation was inspired by Reductor’s breach writeup for DiceCTF 2022. Especially the use of Python 3.10 match statements for pattern matching.
Grok complexity
(please excuse my rambling)
Something I’ve thought about during the course of many CTFs is “what makes a reversing challenge hard to do?”
Usually there are two parts of a reversing problem: first you need to grok (i.e. understand) the problem, then you need to solve it.
For binary-based challenges, grokking usually requires disassembling/decompiling etc… Other times, it may just require understanding what is the program trying to do at a high level. This may be required, for example, to implement a more efficient solver.
Sometimes (if you’re lucky), you can skip the grok phase and blindly throw a binary into angr or throw some data into z3.
For each challenge, the author must put in some amount of effort (I) to construct the challenge (both computational and creative).
The player must then put in some effort (G) to grok the challenge and (S) to solve it.
Presumably, there are some bounds: $$S \le f_s(I)$$ and $$G \le f_g(I)$$ that limit how difficult a problem can be based on the amount of effort required to create it.
The question is what is the order of $f_s$ and $f_g$?
We know from cryptography that we can construct problems that scale exponentially with the amount of work required to construct it (for example integer factorization). So $f_s$ is at least exponential. For practical reasons however, people generally design CTF problems that can be solved within a few hours of reasonable computation.
But how does grok complexity scale with input effort? This is a harder question to answer because it is difficult to quantify.
My theory is that $f_g$ is linear; that is, $G$ is linearly bounded by $I$. In other words, a challenge can’t be harder to grok than it was to create; you can’t get “extra confusion” for free.
However, you can use pre-existing effort to increase the amount of effective construction effort ala Assembly Theory.
For example, a challenge written in C and compiled with gcc has: $$I = I_{challenge} + I_{gcc}$$.
In order to grok this challenge, you need to decompile the program and understand it contextually. In some sense, this can be split into: $$G = G_{challenge} + G_{gcc}$$.
Where $G_{gcc}$ is the effort required to decompile the binary. With modern decompilers, C decompilation is usually pretty good and so you get something like 95% of $G_{gcc}$ for free just by using something like Binary Ninja or IDA.
With other toolchains, you may get more or less “free understanding.” For example, problems written in Rust or Golang are usually much harder to grok because the challenge has the added complexity of understanding large mangled code generated by the respective languages, which existing decompilers are currently not very good at understanding.
This principle captures the intuitive understanding that a problem is harder if there is no existing tooling and easier if there is good, existing tooling.
In the case of compilation/assembly/obfuscation pipelines, the size of code generally scales exponentially with the number of steps taken during construction (steps is roughly linear with effort).
In these situations, the amount of effort required to grok a binary is not linear with respect to the size of the binary but rather logarithmic.
During this challenge, I implemented 11 lifter stages to reduce the code size from 110000 instructions down to ~1500 in order to properly grok it and found it to be a really intersting example of this principle.
Based on the types of patterns I lifted, you could imagine the author writing the same lifts in reverse in order to actually construct the binary and so it shows a very clear linear correlation between $G$ and $I$.
Overview
Ok enough rambling, let’s discuss the challenge:
We are given a serial.c file (where we enter the flag):
char serial[] = "";
A Makefile:
serial:
gcc -shared -o libserial.so serial.c
run:
./eldar
clean:
rm libserial.so > /dev/null
And a binary: eldar which has a really small main function:
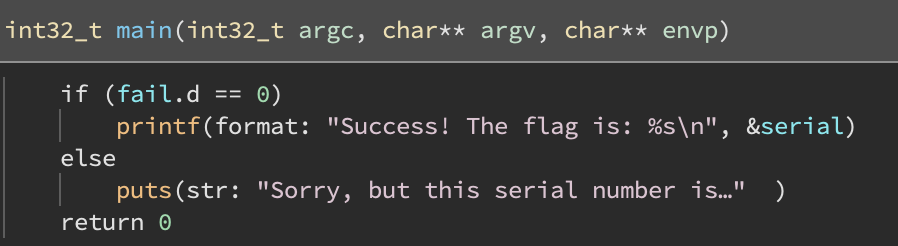
We also see hundreds of thousands of reloactions in eldar:
(objdump -R eldar)
...
00000000009ca49a R_X86_64_RELATIVE *ABS*
000000000080409c R_X86_64_RELATIVE *ABS*+0x00000000008040e4
00000000009ca4fa R_X86_64_COPY ^B@@Base
00000000008040fc R_X86_64_64 ^F@@Base
00000000009ca4fa R_X86_64_RELATIVE *ABS*
000000000080409c R_X86_64_RELATIVE *ABS*+0x00000000008040fc
00000000009ca55a R_X86_64_COPY ^B@@Base
00000000008040fc R_X86_64_64 ^F@@Base
00000000009ca55a R_X86_64_RELATIVE *ABS*
000000000080409c R_X86_64_RELATIVE *ABS*+0x00000000008040e4
00000000009ca5ba R_X86_64_COPY ^B@@Base
00000000008040fc R_X86_64_64 ^F@@Base
...
Evidently fail is somehow being computed during the dynamic linking phase based on serial…
So let’s dive into relocations.
ELF Relocations
- relocations are cool
- relocations are when you, for relocating things
- you can write data
- symbols
- or just numbers
- (sometimes two)
- relocation is for linking, but uh..
- let me start over
- the linker does the relocation with the symbols
- ok, listen...
- just do the relocation please
Dynamic ELF Relocations have a structure like:
typedef struct {
Elf64_Addr r_offset;
Elf64_Xword r_info;
Elf64_Sxword r_addend;
} Elf64_Rela;
And info consists of a type and (optional)symbol reference:
#define ELF64_R_SYM(info) ((info)>>32)
#define ELF64_R_TYPE(info) ((Elf64_Word)(info))
Dynamic symbols will also be relevant and they have the structure:
typedef struct {
Elf64_Word st_name;
unsigned char st_info;
unsigned char st_other;
Elf64_Half st_shndx;
Elf64_Addr st_value;
Elf64_Xword st_size;
} Elf64_Sym;
All relocations write to an address described by r_offset. The value written depends on the relocation type.
(Note lief uses address instead of r_offset so some of my later terminology and code uses r_address. Pls don’t be confused)
There were four types of relocations used in eldar as follows:
REL (type 8)
Set relocation to a base-relative value (but base is always 0):
*(uint64_t *)r.r_offset = r.r_addend;
R64 (type 1)
Set relocation to symbol value + addend:
*(uint64_t *)r.r_offset = symbols[ELF64_R_SYM(r.r_info)] + r.r_addend;
R32 (type 10)
Same as R64 but truncated to 32-bit:
*(uint32_t *)r.r_offset = symbols[ELF64_R_SYM(r.r_info)].st_value + r.r_addend;
CPY (type 5)
Copy N bytes from symbol address into relocation address:
Elf64_Sym sym = symbols[ELF64_R_SYM(r.r_info)];
memcpy(r.r_offset, sym.st_value, sym.st_size);
Part 1: Parsing
I found lief to be pretty nice for parsing relocation data and symbol references.
import lief
from collections import namedtuple
b = lief.ELF.parse('./eldar')
def to_sym(name):
assert len(name) == 1
return ord(name[0])
Rel = namedtuple('REL', ['dst','val','ridx'])
Copy = namedtuple('CPY', ['dst', 'symbol', 'ridx'])
R64 = namedtuple('R64', ['dst','symbol','addend','ridx'])
R32 = namedtuple('R32', ['dst','symbol','addend','ridx'])
def parse(b) -> list:
print('[*] Loading relocations...')
relocs = list(b.relocations)
print('[*] Parsing...')
instructions = []
for i in range(3, len(relocs)):
r = relocs[i]
match r.type:
case 1: # R64
instructions.append(
R64(r.address, to_sym(r.symbol.name), r.addend, i))
case 5: # CPY
instructions.append(
Copy(r.address, to_sym(r.symbol.name), i))
case 8: # REL
instructions.append(
Rel(r.address, r.addend, i))
case 10: # R32
instructions.append(
R32(r.address, to_sym(r.symbol.name), r.addend, i))
return instructions
def dump(instructions):
for op in instructions:
match op:
case Rel(dst, val, ridx):
print(f'[{ridx:04d}] :: rel {dst}, {val}')
case Copy(dst, symbol, ridx):
print(f'[{ridx:04d}] :: copy {dst}, {symbol}')
case R64(dst, symbol, addend, ridx):
print(f'[{ridx:04d}] :: r64 {dst}, {symbol} + {addend}')
case R32(dst, symbol, addend, ridx):
print(f'[{ridx:04d}] :: r64 {dst}, {symbol} + {addend}')
instructions = parse(b)
dump(instructions)
Produces:
...
[0354] :: copy 8405268, 2
[0355] :: rel 8405148, 8405268
[0356] :: rel 8405156, 8
[0357] :: copy 8414226, 2
[0358] :: r64 8405196, 4 + 0
[0359] :: rel 8414226, 0
[0360] :: r64 8405197, 1 + 0
[0361] :: rel 8405148, 8405690
[0362] :: copy 8405244, 2
[0363] :: rel 8405148, 8405196
[0364] :: copy 8414394, 2
[0365] :: r64 8405220, 4 + 0
[0366] :: rel 8414394, 0
[0367] :: rel 8405148, 8405220
[0368] :: copy 8414490, 2
[0369] :: r64 8405220, 5 + 0
[0370] :: rel 8414490, 0
[0371] :: copy 8414562, 2
[0372] :: r64 8405220, 5 + 0
[0373] :: rel 8414562, 0
[0374] :: r64 8405220, 5 + 8405690
[0375] :: copy 8405690, 5
[0376] :: copy 8414666, 2
[0377] :: r64 0, 6 + 0
[0378] :: rel 8405148, 8405698
...
[101463] :: copy 10840770, 2
[101464] :: r64 8405244, 6 + 0
[101465] :: rel 10840770, 0
[101466] :: rel 8405148, 8405244
[101467] :: copy 10840866, 2
[101468] :: r64 8405244, 6 + 0
[101469] :: rel 10840866, 0
[101470] :: rel 8405148, 8405220
[101471] :: copy 10840962, 2
[101472] :: r64 8405244, 6 + 0
[101473] :: rel 10840962, 0
[101474] :: rel 8405148, 8405244
[101475] :: copy 10841058, 2
[101476] :: r64 8405244, 6 + 0
[101477] :: rel 10841058, 0
[101478] :: copy 10841130, 2
[101479] :: r64 8405244, 6 + 0
[101480] :: rel 10841130, 0
[101481] :: rel 8405148, 8405220
More than 100,000 relocations! This also looks pretty unreadable…
What are those values anyways?
At this stage, I noticed that there were some weird reloactions like:
[0377] :: r64 0, 6 + 0
This should be writing to a null pointer, but the program doesn’t crash. So maybe some of the relocations are modifying data as they are executed…
Instead of working with raw numbers, we can check what range the number falls in and assign it a symbolic value if it lies inside the .rela.dyn or .dynsym sections. We also know the flag (serial symbol) is in the range [0x404040:0x40405d] and fail is at 0x404060.
Let’s define our symbolic values:
@dataclass
class Symbol(object):
idx: int
def __repr__(self):
return f's{self.idx}'
@dataclass
class Reloc(object):
idx: int
def __repr__(self):
return f'r{self.idx}'
@dataclass
class Ref(object):
val: Any
def __repr__(self):
return f'&{self.val}'
@dataclass
class SymAddr(object):
sym: Symbol
field: str
def __repr__(self):
return f'{self.sym}.{self.field}'
@dataclass
class RelocAddr(object):
reloc: Reloc
field: str
def __repr__(self):
return f'{self.reloc}.{self.field}'
def vaddr(self):
off = 0
match self.field:
case 'r_address':off = 0
case 'r_info': off = 8
case 'r_addend': off = 16
return (self.reloc.idx * 24) + off + rela.virtual_address
@dataclass
class FlagAddr(object):
idx: int
def __repr__(self):
return f'flag[{self.idx}]'
BaseAddr = namedtuple('baseaddr', [])
FailAddr = namedtuple('fail', [])
And we can implement a format_addr funtion that converts a virtual address into a symbolic value:
rela = [x for x in b.sections if x.name == '.rela.dyn'][0]
dynsym = [x for x in b.sections if x.name == '.dynsym'][0]
def format_addr(addr: int):
if (addr >= rela.virtual_address
and addr < rela.virtual_address + rela.size
):
offset = addr - rela.virtual_address
r_offset = (offset // 24)
r_rem = offset % 24
match r_rem:
case 0: return RelocAddr(Reloc(r_offset), 'r_address')
case 8: return RelocAddr(Reloc(r_offset), 'r_info')
case 16: return RelocAddr(Reloc(r_offset), 'r_addend')
case _: return RelocAddr(Reloc(r_offset), r_rem)
elif (addr > dynsym.virtual_address
and addr < dynsym.virtual_address + dynsym.size
):
offset = addr - dynsym.virtual_address
r_offset = (offset // 24)
r_rem = offset % 24
match r_rem:
case 0: return SymAddr(Symbol(r_offset), 'st_name')
case 8: return Symbol(r_offset)
case 16: return SymAddr(Symbol(r_offset), 'st_size')
case _: return SymAddr(Symbol(r_offset), r_rem)
elif addr >= 0x404040 and addr < 0x404040+29:
off = addr-0x404040
return FlagAddr(off)
elif addr == 0x804000:
return BaseAddr()
elif addr == 0x404060:
return FailAddr()
else:
return addr
While parsing, we will call format_address on every numeric value first (not shown here). We get something like the following:
// Interesting section of NOPs:
[0083] :: rel baseaddr(), 0
[0084] :: rel baseaddr(), 0
[0085] :: rel baseaddr(), 0
[0086] :: rel baseaddr(), 0
[0087] :: rel baseaddr(), 0
[0088] :: rel baseaddr(), 0
[0089] :: rel baseaddr(), 0
// Writing some consecutive values into previously
// applied relocations:
[0090] :: rel r3.r_address, 0
[0091] :: rel r3.r_info, 1
[0092] :: rel r3.r_addend, 2
[0093] :: rel r4.r_address, 3
[0094] :: rel r4.r_info, 4
[0095] :: rel r4.r_addend, 5
[0096] :: rel r5.r_address, 6
[0097] :: rel r5.r_info, 7
[0098] :: rel r5.r_addend, 8
[0099] :: rel r6.r_address, 9
[0100] :: rel r6.r_info, 10
[0101] :: rel r6.r_addend, 11
// Much more readable code!
[0343] :: rel r87.r_info, 253
[0344] :: rel r87.r_addend, 254
[0345] :: rel r88.r_address, 255
[0346] :: rel s4, 0
[0347] :: rel s2, r3.r_address
[0348] :: rel s2.st_size, 8
[0349] :: copy r350.r_addend, s2
[0350] :: r64 s4, s4 + 0
[0351] :: rel r350.r_addend, 0
[0352] :: rel s2, flag[0]
[0353] :: rel s2.st_size, 1
We can also see stuff like:
[0349] :: copy r350.r_addend, s2
[0350] :: r64 s4, s4 + 0
Relocation 349 is overwriting the addend in relocation 350. Effectively, this pair is performing s4 += s2 (the 0 in the addend is overwritten with the value of s2).
We also see a similiar pattern for overwriting addresses:
[0376] :: copy r377.r_address, s2
[0377] :: r64 0, s6 + 0
I.e. s2 = s6.
We could probably get some cleaner code if we pattern match on these structures and define higher level operations…
Part 2: Do you even lift bro?
Now for the fun part!
1. Arr + Out references
During parsing, I noticed some relocations were acting as NOPs (writing 0 to a fixed address). And other relocations were storing arbitrary values in those relococation spots (like a uin64_t array).
Specifically, it seems like r3 to r88 are being used as an array. Also r89 seems to be some sort of output value (will get to that later).
We can modify format_addr to understand these references:
@dataclass
class OutAddr(object):
idx: int
def __repr__(self):
return f'out[{self.idx}]'
@dataclass
class ArrAddr(object):
idx: int
def __repr__(self):
return f'arr[{self.idx}]'
def format_addr(addr: int):
if (addr >= rela.virtual_address
and addr < rela.virtual_address + rela.size
):
offset = addr - rela.virtual_address
r_offset = (offset // 24)
r_rem = offset % 24
# --- NEW ---
if r_offset >= 3 and r_offset <= 88:
arr_idx = (r_offset - 3) * 3 + (r_rem // 8)
return ArrAddr(arr_idx)
elif r_offset == 89:
return OutAddr(r_rem)
# --- END ---
match r_rem:
# ...
Sample 1 (102000 instructions)
// Nice array references!
[0338] :: rel arr[248], 248
[0339] :: rel arr[249], 249
[0340] :: rel arr[250], 250
[0341] :: rel arr[251], 251
[0342] :: rel arr[252], 252
[0343] :: rel arr[253], 253
[0344] :: rel arr[254], 254
[0345] :: rel arr[255], 255
[0346] :: rel s4, 0
[0347] :: rel s2, arr[0] // neat
[0348] :: rel s2.st_size, 8
[0349] :: copy r350.r_addend, s2
[0350] :: r64 s4, s4 + 0
[0351] :: rel r350.r_addend, 0
[0352] :: rel s2, flag[0] // flag!
[0353] :: rel s2.st_size, 1
[0354] :: copy s7, s2
[0355] :: rel s2, s7
[0356] :: rel s2.st_size, 8
[0357] :: copy r358.r_addend, s2
[0358] :: r64 s4, s4 + 0
[0359] :: rel r358.r_addend, 0
[0360] :: r64 s4.9, s1 + 0
[0361] :: rel s2, arr[0]
[0362] :: copy s6, s2
Much nicer!
2. Mov + Add
Next we can replace Rel, R64 and Copy with the more understandable Mov and Add.
In order to know the size of the mov (can vary with Copy), we need to first trace through all the instructions and keep track of symbol sizes at each offset. We can just look for writes to a symbols st_size to see those changes. Luckily they are deterministic in this program.
Mov = namedtuple('mov', ['dst', 'src', 'sz', 'ridx'])
Add = namedtuple('add', ['dst', 'src', 'addend', 'ridx'])
def lift_mov_add(instructions):
idx = 0
sizes = []
curr = [8] * 8
sizes.append(curr)
# Trace instructions and monitor the size of every symbol.
for instr in instructions:
c = list(curr)
match instr:
case Rel(SymAddr(Symbol(idx), 'st_size'), val, ridx):
c[idx] = val
sizes.append(c)
# Iterate and find Mov/Add patterns.
while idx < len(instructions):
match instructions[idx]:
case Rel(dst, val, ridx):
instructions[idx] = Mov(dst, Ref(val), 8, ridx)
case Copy(dst, sym, ridx):
instructions[idx] = Mov(
dst, sym, sizes[idx][sym.idx], ridx)
case R64(dst, sym, add, ridx):
instructions[idx] = Add(dst, sym, add, ridx)
idx += 1
return instructions
def remove_sizes(instructions):
# Sizes are now nops.
idx = 0
while idx < len(instructions):
match instructions[idx]:
case Mov(SymAddr(Symbol(s), 'st_size'), _, _, _):
instructions[idx:idx+1] = []
idx += 1
return instructions
We also need to update our dump function to support these new types:
def dump(instructions):
for op in instructions:
match op:
# --- snip ---
case Mov(dst, src, 8, ridx):
print(f'[{ridx:04d}] :: mov {dst}, {src}')
case Mov(dst, src, sz, ridx):
print(f'[{ridx:04d}] :: mov({sz}) {dst}, {src}')
case Add(dst, src, add, ridx):
print(f'[{ridx:04d}] :: add {dst}, {src}, {add}')
For the rest of the writeup, I’ll omit changes to dump; just imagine we are also implementing print formats.
Sample 2 (96179 instructions)
// smoooth
[0336] :: mov arr[246], &246
[0337] :: mov arr[247], &247
[0338] :: mov arr[248], &248
[0339] :: mov arr[249], &249
[0340] :: mov arr[250], &250
[0341] :: mov arr[251], &251
[0342] :: mov arr[252], &252
[0343] :: mov arr[253], &253
[0344] :: mov arr[254], &254
[0345] :: mov arr[255], &255
[0346] :: mov s4, &0
[0347] :: mov s2, &arr[0]
[0349] :: mov r350.r_addend, s2
[0350] :: add s4, s4, 0
[0351] :: mov r350.r_addend, &0
[0352] :: mov s2, &flag[0]
[0354] :: mov(1) s7, s2
[0355] :: mov s2, &s7
[0357] :: mov r358.r_addend, s2
[0358] :: add s4, s4, 0
[0359] :: mov r358.r_addend, &0
[0360] :: r64 s4.9, s1 + 0
[0361] :: mov s2, &arr[0]
[0362] :: mov s6, s2
[0363] :: mov s2, &s4
3. Indirect mov
As mentioned before, there are some cases where the r_addend of a subsequent relocation is modified before it is applied. For example:
[0349] :: mov r350.r_addend, s2
[0350] :: add s4, s4, 0
[0351] :: mov r350.r_addend, &0
This triplet is just s4 = s2. I think the third instruction (resetting r_addend) is an artifact of how the program was compiled, I don’t think it’s actually necessary.
Using Python 3.10 match ❤️, we can perform really clean pattern matching on this type of structure and replace it with a single Add instruction:
def lift_indirect(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+3]:
case [
Mov(RelocAddr(Reloc(r1), 'r_addend'), sym, _, ridx_1),
Add(dst_2, sym_2, _, ridx_2),
Mov(RelocAddr(Reloc(r3), 'r_addend'), Ref(0), _, _),
] if (
(r1 == ridx_2) and (r3 == ridx_2)
):
instructions[idx:idx+3] = [
Add(dst_2, sym_2, sym, ridx_1)
]
idx += 1
return instructions
Sample 3 (58155 instructions)
[0346] :: mov s4, &0
[0347] :: mov s2, &arr[0]
[0349] :: add s4, s4, s2 // wow
[0352] :: mov s2, &flag[0]
[0354] :: mov(1) s7, s2
[0355] :: mov s2, &s7
[0357] :: add s4, s4, s2 // cool
[0360] :: r64 s4.9, s1 + 0
[0361] :: mov s2, &arr[0]
[0362] :: mov s6, s2
[0363] :: mov s2, &s4
[0364] :: add s5, s4, s2 // amazing
[0367] :: mov s2, &s5
4. Block
Examining the disassembly, we can spot a repeating block of code:
// ---------------
[0378] :: mov s2, &arr[1]
[0379] :: add s4, s4, s2
[0382] :: mov s2, &flag[1]
[0384] :: mov(1) s7, s2
[0385] :: mov s2, &s7
[0387] :: add s4, s4, s2
[0390] :: r64 s4.9, s1 + 0
[0391] :: mov s2, &arr[1]
[0392] :: mov s6, s2
[0393] :: mov s2, &s4
[0394] :: add s5, s4, s2
[0397] :: mov s2, &s5
[0398] :: add s5, s5, s2
[0401] :: add s5, s5, s2
[0404] :: add s5, s5, arr[0]
[0405] :: mov arr[1], s5
[0406] :: mov r407.r_address, s2
[0407] :: add 0, s6, 0
// ---------------
[0408] :: mov s2, &arr[2]
[0409] :: add s4, s4, s2
[0412] :: mov s2, &flag[0]
[0414] :: mov(1) s7, s2
[0415] :: mov s2, &s7
[0417] :: add s4, s4, s2
[0420] :: r64 s4.9, s1 + 0
[0421] :: mov s2, &arr[2]
[0422] :: mov s6, s2
[0423] :: mov s2, &s4
[0424] :: add s5, s4, s2
[0427] :: mov s2, &s5
[0428] :: add s5, s5, s2
[0431] :: add s5, s5, s2
[0434] :: add s5, s5, arr[0]
[0435] :: mov arr[2], s5
[0436] :: mov r437.r_address, s2
[0437] :: add 0, s6, 0
// ---------------
These blocks do:
# ---
s6 = (s6 + arr[1] + flag[1]) & 0xff
arr[1], arr[s6] = arr[s6], arr[1]
# ---
s6 = (s6 + arr[2] + flag[0]) & 0xff
arr[2], arr[s6] = arr[s6], arr[2]
# ---
The only things that seem to change are the arr and flag indexes used. We can lift it!
Block = namedtuple('block', ['arr', 'flag', 'ridx'])
def lift_block(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+18]:
case [
Mov(_,arr,_,ridx),
Add(_,_,_,_),
Mov(_,flag,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
R32(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Add(_,_,_,_),
Add(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
]:
instructions[idx:idx+18] = [
Block(arr, flag, ridx)
]
idx += 1
return instructions
Sample 4 (23339 instructions)
// array set
[0342] :: mov arr[252], &252
[0343] :: mov arr[253], &253
[0344] :: mov arr[254], &254
[0345] :: mov arr[255], &255
// s4 = 0
[0346] :: mov s4, &0
// repeating shuffles...
[0347] :: shuffle &arr[0], &flag[0]
[0378] :: shuffle &arr[1], &flag[1]
[0408] :: shuffle &arr[2], &flag[0]
[0438] :: shuffle &arr[3], &flag[1]
[0468] :: shuffle &arr[4], &flag[0]
[0498] :: shuffle &arr[5], &flag[1]
[0528] :: shuffle &arr[6], &flag[0]
// later
[24275] :: add s5, s5, s2
[24278] :: add s5, s5, s2
[24281] :: add s5, s5, arr[0]
[24282] :: mov out[8], s5
// array is reset again...
[24283] :: mov arr[0], &0
[24284] :: mov arr[1], &1
[24285] :: mov arr[2], &2
[24286] :: mov arr[3], &3
[24287] :: mov arr[4], &4
[24288] :: mov arr[5], &5
[24289] :: mov arr[6], &6
[24290] :: mov arr[7], &7
[24291] :: mov arr[8], &8
[24292] :: mov arr[9], &9
[24293] :: mov arr[10], &10
[24294] :: mov arr[11], &11
5. Reset + ShuffleBlock
Since the array initialization seems to happen multiple times, lets lift that too. We can also lift the series of shuffle instructions:
Reset = namedtuple('reset', ['ridx'])
ShuffleBlock = namedtuple('shuffleblock', ['f1', 'f2', 'ridx'])
def lift_reset(instructions):
idx = 0
while idx < len(instructions) - 256:
good = True
for i in range(256):
op = instructions[idx+i]
if type(op) == Mov:
dst, src, _, _ = op
if dst != ArrAddr(i) or src != Ref(i):
good = False
break
else:
good = False
break
if good:
instructions[idx:idx+256] = [
Reset(instructions[idx].ridx)
]
idx += 1
return instructions
def lift_shuffle_block(instructions):
idx = 0
while idx < len(instructions) - 256:
good = True
for i in range(256):
op = instructions[idx+i]
if type(op) == Block:
arr, flag, ridx = op
if arr != Ref(ArrAddr(i)):
good = False
break
else:
good = False
break
if good:
instructions[idx:idx+256] = [
ShuffleBlock(
instructions[idx].flag,
instructions[idx+1].flag,
instructions[idx].ridx)]
idx += 1
return instructions
Sample 5 (19259 instructions)
[0090] :: reset // wow
[0346] :: mov s4, &0
[0347] :: shuffleblock &flag[0], &flag[1] // so smol
[8028] :: mov s4, &0
[8029] :: mov s2, &arr[0]
[8030] :: add s4, s4, s2
[8033] :: r32 s4.9, s1, 0
// ...
[8154] :: mov out[2], s5
[8155] :: reset
[8411] :: mov s4, &0
[8412] :: shuffleblock &flag[2], &flag[3] // another!
[16092] :: mov s4, &0
[16093] :: mov s2, &arr[0]
[16094] :: add s4, s4, s2
[16097] :: r32 s4.9, s1, 0
6. Output
In between each reset/shuffleblock pair, there are three repeating blocks of instructions that seem to write to the out area:
// ---------------
[8029] :: mov s2, &arr[0]
[8030] :: add s4, s4, s2
[8033] :: r32 s4.9, s1, 0
[8034] :: mov s6, s2
[8035] :: mov s2, &s4
[8036] :: add s5, s4, s2
[8039] :: mov s2, &s5
[8040] :: add s5, s5, s2
[8043] :: add s5, s5, s2
[8046] :: add s5, s5, arr[0]
[8047] :: mov arr[0], s5
[8048] :: mov s2, &arr[0]
[8049] :: mov s7, s2
[8050] :: mov s2, &s5
[8051] :: mov r8052.r_address, s2
[8052] :: add 0, s6, 0
[8053] :: mov s2, &s7
[8054] :: add s6, s6, s2
[8057] :: r32 s6.9, s1, 0
[8058] :: mov s2, &s6
[8059] :: add s5, s6, s2
[8062] :: mov s2, &s5
[8063] :: add s5, s5, s2
[8066] :: add s5, s5, s2
[8069] :: add s5, s5, arr[0]
[8070] :: mov out[0], s5
// ---------------
[8071] :: mov s2, &arr[1]
[8072] :: add s4, s4, s2
[8075] :: r32 s4.9, s1, 0
[8076] :: mov s6, s2
[8077] :: mov s2, &s4
[8078] :: add s5, s4, s2
[8081] :: mov s2, &s5
[8082] :: add s5, s5, s2
[8085] :: add s5, s5, s2
[8088] :: add s5, s5, arr[0]
[8089] :: mov arr[1], s5
[8090] :: mov s2, &arr[1]
[8091] :: mov s7, s2
[8092] :: mov s2, &s5
[8093] :: mov r8094.r_address, s2
[8094] :: add 0, s6, 0
[8095] :: mov s2, &s7
[8096] :: add s6, s6, s2
[8099] :: r32 s6.9, s1, 0
[8100] :: mov s2, &s6
[8101] :: add s5, s6, s2
[8104] :: mov s2, &s5
[8105] :: add s5, s5, s2
[8108] :: add s5, s5, s2
[8111] :: add s5, s5, arr[0]
[8112] :: mov out[1], s5
// ---------------
These are doing:
# ---
s4 = (s4 + arr[0]) & 0xff
arr[0], arr[s4] = arr[s4], arr[0]
out[0] = arr[(arr[0] + arr[s4]) & 0xff]
# ---
s4 = (s4 + arr[1]) & 0xff
arr[1], arr[s4] = arr[s4], arr[1]
out[1] = arr[(arr[1] + arr[s4]) & 0xff]
# ---
Let’s lift them:
Output = namedtuple('output', ['out', 'arr', 'ridx'])
def lift_output(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+26]:
case [
Mov(_,arr,_,ridx),
Add(_,_,_,_),
R32(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Add(_,_,_,_),
Add(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
R32(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Mov(_,_,_,_),
Add(_,_,_,_),
Add(_,_,_,_),
Add(_,_,_,_),
Mov(out,_,_,_),
]:
instructions[idx:idx+26] = [Output(out, arr, ridx)]
idx += 1
return instructions
Sample 6 (18659 instructions)
// hey this is looking almost readable
[0090] :: reset
[0346] :: mov s4, &0
[0347] :: shuffleblock &flag[0], &flag[1]
[8028] :: mov s4, &0
[8029] :: output out[0], &arr[0] // neat
[8071] :: output out[1], &arr[1]
[8113] :: output out[2], &arr[2]
[8155] :: reset
[8411] :: mov s4, &0
[8412] :: shuffleblock &flag[2], &flag[3]
[16092] :: mov s4, &0
[16093] :: output out[3], &arr[0]
[16135] :: output out[4], &arr[1]
[16177] :: output out[5], &arr[2]
[16219] :: reset
[16475] :: mov s4, &0
[16476] :: shuffleblock &flag[4], &flag[5]
[24156] :: mov s4, &0
[24157] :: output out[6], &arr[0]
[24199] :: output out[7], &arr[1]
[24241] :: output out[8], &arr[2]
[24283] :: reset
[24539] :: mov s4, &0
[24540] :: shuffleblock &flag[6], &flag[7]
[32220] :: mov s4, &0
[32221] :: output out[9], &arr[0]
[32263] :: output out[10], &arr[1]
[32305] :: output out[11], &arr[2]
[32347] :: reset
[32603] :: mov s4, &0
7. MultAdd
After we get through flag[16], these patterns stop and we get some new code.
We encounter these new blocks but they don’t seem to be identical:
/ ----------
[64730] :: mov s2, &out[2]
[64732] :: mov(1) s5, s2
[64733] :: mov s6, &0
[64734] :: mov s2, &s6
[64736] :: add s6, s6, s2
[64739] :: mov s2, &s5
[64740] :: add s6, s6, s2
[64743] :: mov s2, &s6
[64744] :: add s6, s6, s2
[64747] :: mov s2, &s5
[64748] :: add s6, s6, s2
[64751] :: mov s2, &s6
[64752] :: add s6, s6, s2
[64755] :: add s6, s6, s2
[64758] :: mov s2, &s5
[64759] :: add s6, s6, s2
[64762] :: mov s2, &s6
[64763] :: add s6, s6, s2
[64766] :: add s6, s6, s2
[64769] :: add s6, s6, s2
[64772] :: add s6, s6, s2
[64775] :: add s7, s7, s2
// ----------
[64778] :: mov s2, &out[3]
[64780] :: mov(1) s5, s2
[64781] :: mov s6, &0
[64782] :: mov s2, &s6
[64784] :: add s6, s6, s2
[64787] :: mov s2, &s5
[64788] :: add s6, s6, s2
[64791] :: mov s2, &s6
[64792] :: add s6, s6, s2
[64795] :: mov s2, &s5
[64796] :: add s6, s6, s2
[64799] :: mov s2, &s6
[64800] :: add s6, s6, s2
[64803] :: mov s2, &s5
[64804] :: add s6, s6, s2
[64807] :: mov s2, &s6
[64808] :: add s6, s6, s2
[64811] :: mov s2, &s5
[64812] :: add s6, s6, s2
[64815] :: mov s2, &s6
[64816] :: add s6, s6, s2
[64819] :: add s6, s6, s2
[64822] :: mov s2, &s5
[64823] :: add s6, s6, s2
[64826] :: mov s2, &s6
[64827] :: add s6, s6, s2
[64830] :: mov s2, &s5
[64831] :: add s6, s6, s2
[64834] :: mov s2, &s6
[64835] :: add s7, s7, s2
/ ----------
The blocks work like this:
// s5 = out[3]
[64778] :: mov s2, &out[3]
[64780] :: mov(1) s5, s2
[64781] :: mov s6, &0
// compute some multiple of s5
// add result to s7
[64835] :: add s7, s7, s2
The inner multiple bit works by perforing either s6 += s5 (add value) or s6 += s6 (double current value).
For example:
[64730] :: mov s2, &out[2]
[64732] :: mov(1) s5, s2 // s5 = out[2]
[64733] :: mov s6, &0 // s6 = 0
[64734] :: mov s2, &s6
[64736] :: add s6, s6, s2 // s6 = 0
[64739] :: mov s2, &s5
[64740] :: add s6, s6, s2 // s6 = out[2]
[64743] :: mov s2, &s6
[64744] :: add s6, s6, s2 // s6 = 2 * out[2]
[64747] :: mov s2, &s5
[64748] :: add s6, s6, s2 // s6 = 3 * out[2]
[64751] :: mov s2, &s6
[64752] :: add s6, s6, s2 // s6 = 6 * out[2]
[64755] :: add s6, s6, s2 // s6 = 12 * out[2]
[64758] :: mov s2, &s5
[64759] :: add s6, s6, s2 // s6 = 13 * out[2]
[64762] :: mov s2, &s6
[64763] :: add s6, s6, s2 // s6 = 26 * out[2]
[64766] :: add s6, s6, s2 // s6 = 52 * out[2]
[64769] :: add s6, s6, s2 // s6 = 104 * out[2]
[64772] :: add s6, s6, s2 // s6 = 208 * out[2]
[64775] :: add s7, s7, s2 // s7 += (208 * out[2])
It takes a bit more work but we can also lift these operations:
MultAdd = namedtuple('multadd', ['out', 'val', 'k', 'ridx'])
def lift_multadd(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+3]:
# block prefix
case [
Mov(Symbol(2), out, _, ridx),
Mov(Symbol(5), Symbol(2), _, _),
Mov(Symbol(6), Ref(0), _, _),
]:
k = 0
double = False
ptr = idx + 3
good = True
while ptr < len(instructions):
match instructions[ptr]:
case Mov(Symbol(2), Ref(Symbol(6)), _, _):
double = True
case Mov(Symbol(2), Ref(Symbol(5)), _, _):
double = False
case Add(Symbol(6), Symbol(6), Symbol(2), _):
k = (k * 2) if double else (k + 1)
case Add(Symbol(7), Symbol(7), Symbol(2), _):
ptr += 1
break
case _:
good = False
break
ptr += 1
if good:
instructions[idx:ptr] = [
MultAdd(Symbol(7), out, k, ridx)
]
idx += 1
return instructions
Sample 7 (2377 instructions)
[56795] :: mov s4, &0
[56796] :: shuffleblock &flag[14], &flag[15]
[64476] :: mov s4, &0
[64477] :: output out[21], &arr[0]
[64519] :: output out[22], &arr[1]
[64561] :: output out[23], &arr[2]
[64603] :: mov s2, &r101917.r_address
[64605] :: mov(2064) arr[0], s2
[64606] :: mov s4, &0
[64607] :: mov s5, &0
[64608] :: mov s7, &-393039
[64609] :: madd s7 += (&out[0] * 155) // math!
[64667] :: madd s7 += (&out[1] * 190)
[64730] :: madd s7 += (&out[2] * 208)
[64778] :: madd s7 += (&out[3] * 123)
[64838] :: madd s7 += (&out[4] * 214)
[64896] :: madd s7 += (&out[5] * 146)
[64944] :: madd s7 += (&out[6] * 211)
[65002] :: madd s7 += (&out[7] * 85)
[65052] :: madd s7 += (&out[8] * 87)
[65107] :: madd s7 += (&out[9] * 251)
[65175] :: madd s7 += (&out[10] * 122)
[65230] :: madd s7 += (&out[11] * 60)
[65277] :: madd s7 += (&out[12] * 237)
[65340] :: madd s7 += (&out[13] * 27)
[65384] :: madd s7 += (&out[14] * 63)
[65441] :: madd s7 += (&out[15] * 207)
[65504] :: madd s7 += (&out[16] * 33)
[65541] :: madd s7 += (&out[17] * 138)
[65589] :: madd s7 += (&out[18] * 51)
[65636] :: madd s7 += (&out[19] * 103)
[65691] :: madd s7 += (&out[20] * 58)
[65738] :: madd s7 += (&out[21] * 68)
[65778] :: madd s7 += (&out[22] * 120)
[65828] :: madd s7 += (&out[23] * 111)
[65888] :: mov s2, &s5.11
[65890] :: mov(5) s7.11, s2
[65891] :: mov s2, &s7
[65893] :: add s4, s4, s2
[65896] :: mov s7, &-368502
[65897] :: madd s7 += (&out[0] * 254)
[65965] :: madd s7 += (&out[1] * 21)
[66004] :: madd s7 += (&out[2] * 157)
[66062] :: madd s7 += (&out[3] * 204)
[66115] :: madd s7 += (&out[4] * 56)
[66157] :: madd s7 += (&out[5] * 134)
8. Trunc
After each set of madd ops, we see some weird instructions:
[65888] :: mov s2, &s5.11
[65890] :: mov(5) s7.11, s2
We are writing to an 11-byte offset of a symbol which means &sym.st_value + 3.
Examining the code, we see that s5 is always zero. So this instruction is just zeroing the upper 5 bytes of the symbol value. In other words sym &= 0xffffff.
Trunc = namedtuple('trunc', ['val', 'k', 'ridx'])
def lift_truncate(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+2]:
case [
Mov(Symbol(2), Ref(SymAddr(Symbol(5), 11)), _, ridx),
Mov(SymAddr(Symbol(7), 11), Symbol(2), 5, _)
]:
instructions[idx:idx+2] = [
Trunc(Symbol(7), 0xffffff, ridx)]
idx += 1
return instructions
Sample 8 (2336 instructions)
[80967] :: madd s7 += (&out[17] * 219)
[81030] :: madd s7 += (&out[18] * 74)
[81075] :: madd s7 += (&out[19] * 223)
[81143] :: madd s7 += (&out[20] * 220)
[81201] :: madd s7 += (&out[21] * 235)
[81264] :: madd s7 += (&out[22] * 151)
[81322] :: madd s7 += (&out[23] * 165)
[81375] :: trunc s7 &= 0xffffff // yay
[81378] :: mov s2, &s7
[81380] :: add s4, s4, s2
[81383] :: mov s7, &-488931
[81384] :: madd s7 += (&out[0] * 207)
[81447] :: madd s7 += (&out[1] * 123)
[81507] :: madd s7 += (&out[2] * 9)
9. Array slots
Looking at this new bytecode, we see a ton of scary constants. And some new places that look like they might be arrays:
Note: setinfo is just an 8-byte mov into the symbol st_name field which sets various other fields.
// NOP relocations for array space
[93678] :: mov baseaddr(), &0
[93679] :: mov baseaddr(), &0
[93680] :: mov baseaddr(), &0
[93681] :: mov baseaddr(), &0
[93682] :: mov baseaddr(), &0
[93683] :: mov baseaddr(), &0
// Array data...
[93684] :: mov r93678.r_address, &6124966137932793672
[93685] :: mov r93678.r_info, &-4041842636978026168
[93686] :: mov r93678.r_addend, &5027987508982512709
[93687] :: mov r93679.r_address, &-8413873093579112200
[93688] :: mov r93679.r_info, &5011179070235933765
[93689] :: mov r93679.r_addend, &4323655821306185960
[93690] :: mov r93680.r_address, &7154245383694349856
[93691] :: mov r93680.r_info, &-3458402876407461680
[93692] :: mov r93680.r_addend, &-5186046161349200369
[93693] :: mov r93681.r_address, &51797902590214145
[93694] :: mov r93681.r_info, &5009120185953550336
[93695] :: mov r93681.r_addend, &-4648246994148326916
[93696] :: mov r93682.r_address, &-8410243179269569141
[93697] :: mov r93682.r_info, &51245831810508869
[93698] :: mov r93682.r_addend, &5011371985779865103
[93699] :: mov r93683.r_address, &215243856300280
[93700] :: mov s3, &r93678.r_address
[93701] :: setinfo s3, name=0x1a, info=0x1, other=0x0, shndx=0x0
[93702] :: add s5, s3, 0
[93703] :: mov s2, &r101997.r_address
[93705] :: mov(144) r93678.r_address, s2
[93706] :: mov s2, &s5
[93708] :: add s4, s4, s2
[93711] :: mov s5, &0
[93712] :: mov s7, &-55708
[93713] :: madd s7 += (&flag[16] * 76)
[93758] :: madd s7 += (&flag[17] * 104)
[93803] :: mov s2, &flag[18]
[93805] :: mov(1) s5, s2
// Array space?
[93806] :: mov baseaddr(), &0
// Array data...
[93807] :: mov r93806.r_address, &-6989445605485108096
[93808] :: mov r93806.r_info, &195
[93809] :: mov s3, &r93806.r_address
[93810] :: setinfo s3, name=0x1a, info=0x1, other=0x0, shndx=0x0
[93811] :: add r93806.r_address, s3, 0
[93812] :: mov s2, &r102002.r_address
[93814] :: mov(24) r93806.r_address, s2
[93815] :: mov s2, &s5
These arrays always seem to consist of a bunch of nop instructions (mov baseaddr(), &0) followed by mov’s into the array with constant values.
We can scan bytecode for these patterns and lift into a fixed constant array:
ArraySlots = namedtuple('arr', ['values', 'ridx'])
def lift_array_slots(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx]:
case Mov(BaseAddr(), Ref(0), _, ridx):
ptr = idx+1
while ptr < len(instructions):
op = instructions[ptr]
if type(op) != Mov or op.dst != BaseAddr():
break
ptr += 1
start = idx
end = ptr
data = []
# Check for movs into array.
vstart = RelocAddr(Reloc(ridx), 'r_address').vaddr()
offset = 0
while end + offset < len(instructions) and offset < ((end - start) * 3):
op = instructions[end + offset]
if type(op) == Mov and type(op.dst) is RelocAddr and op.dst.vaddr() == vstart + (offset * 8):
data.append(op.src.val)
else:
break
offset += 1
if len(data) > 0:
data += [0] * (((end - start) * 3) - len(data))
instructions[idx:end+offset] = [
ArraySlots(data, ridx)
]
idx += 1
return instructions
Sample 9 (2161 instructions)
[93677] :: mov s5, &0
// what a chonker
[93678] :: array [0x5500404040c7c748, -0x38178276b71a76b8, 0x45c700000000fc45, -0x74c414ffffffff08, 0x458b48d06348fc45, 0x3c00b60fd00148e8, 0x6348fc458b147620, -0x2ffeb717ba74b730, -0x47f88981c3ff49f1, 0xb805eb00000001, 0x4583f84509000000, -0x4081e403827cfe04, -0x74b72f9cb703ba75, 0xb60fd00148e845, 0x458bf84509c0b60f, 0xc3c35d9848f8, 0x0, 0x0]
[93700] :: mov s3, &r93678.r_address
[93701] :: setinfo s3, name=0x1a, info=0x1, other=0x0, shndx=0x0
[93702] :: add s5, s3, 0
[93703] :: mov s2, &r101997.r_address
[93705] :: mov(144) r93678.r_address, s2
[93706] :: mov s2, &s5
[93708] :: add s4, s4, s2
[93711] :: mov s5, &0
[93712] :: mov s7, &-55708
[93713] :: madd s7 += (&flag[16] * 76)
[93758] :: madd s7 += (&flag[17] * 104)
[93803] :: mov s2, &flag[18]
[93805] :: mov(1) s5, s2
// smol
[93806] :: array [-0x60ff7fbf1bdadb80, 0xc3, 0x0]
[93809] :: mov s3, &r93806.r_address
[93810] :: setinfo s3, name=0x1a, info=0x1, other=0x0, shndx=0x0
[93811] :: add r93806.r_address, s3, 0
[93812] :: mov s2, &r102002.r_address
10. Shellcode
Now wtf are those values? At first I thought they might be constant target values for some matrix computations.
But I couldn’t help but noticing the 0x48 prefix and 0xc3 suffix and got suspicious about bytecode. I had also noticed earlier that the relocation section was marked rwx.
So let’s throw this first chunk into Binary Ninja and see what happens…
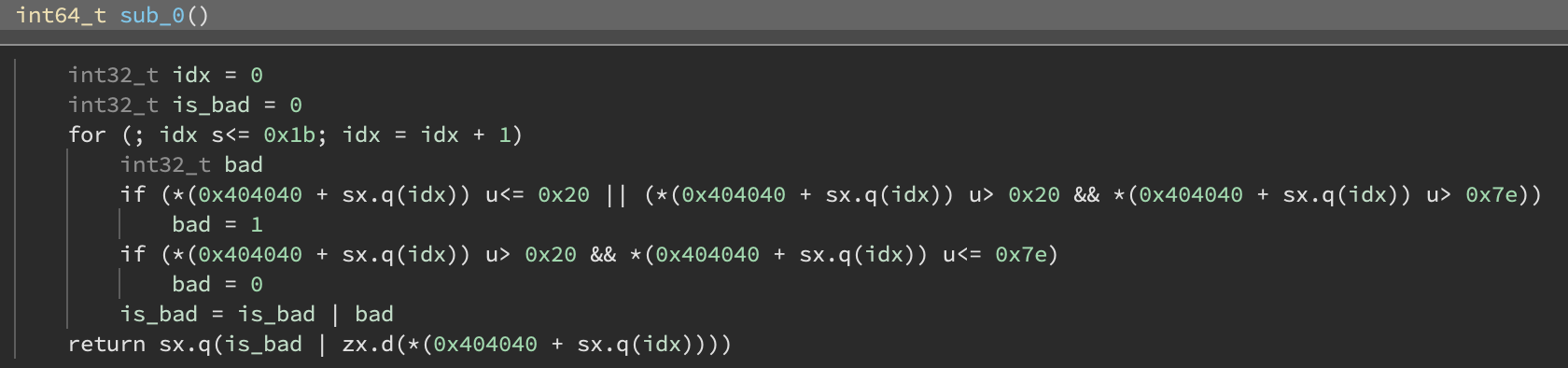
Well… that is certainly bytecode. This first large function seems to just be checking that all the flag bytes are in range (0x20, 0x7e).
This is also the only big function, the rest seem to all be 9-byte shellcode data.
I don’t really understand how the shellcode is actually being executed here, but it has something to do with loading a symbol that points to the shellcode. We can recognize the following blocks as an “execute shellcode” block:
[93806] :: array [-0x60ff7fbf1bdadb80, 0xc3, 0x0]
[93809] :: mov s3, &r93806.r_address
[93810] :: setinfo s3, name=0x1a, info=0x1, other=0x0, shndx=0x0
[93811] :: add r93806.r_address, s3, 0
[93812] :: mov s2, &r102002.r_address
[93814] :: mov(24) r93806.r_address, s2
Let’s lift!
from capstone import *
md = Cs(CS_ARCH_X86, CS_MODE_64)
# ---
Shellcode = namedtuple('shellcode', ['dst', 'code', 'ridx'])
def lift_shellcode(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+6]:
case [
ArraySlots(values, ridx),
Mov(Symbol(3), Ref(RelocAddr(Reloc(rel2), 'r_address')), _, _),
Mov(SymAddr(Symbol(3), 'st_name'), _, _, _),
Add(dst, Symbol(3), _, _),
Mov(Symbol(2), _, _, _),
Mov(RelocAddr(Reloc(rel6), 'r_address'), Symbol(2), _, _)
] if (rel2 == ridx) and (rel6 == ridx):
instructions[idx:idx+6] = [
Shellcode(dst, b''.join([(x & 0xffffffffffffffff).to_bytes(8, 'little') for x in values]), ridx)
]
idx += 1
return instructions
And we can also get fancy and disassemble with capstone when we dump:
def dump(instructions):
# ...
case Shellcode(dst, code, ridx):
print(f'[{ridx:04d}] :: exec {dst} <- {code.hex()}')
print('-' * 20)
for i in md.disasm(code, 0):
if i.mnemonic == 'ret':
break
print(" 0x%x:\t%s\t%s" % (
i.address,
i.mnemonic,
i.op_str.replace('0x8040e4', 's5')
.replace('0x8040cc', 's4')))
print('-' * 20)
Sample 10 (1771 instructions)
// have you seen sexier disassembly?
[100408] :: add s4, s4, s2
[100411] :: mov s7, &-30801
[100412] :: madd s7 += (&flag[16] * 15)
[100453] :: madd s7 += (&flag[17] * 41)
[100495] :: mov s2, &flag[18]
[100497] :: mov(1) s5, s2
[100498] :: exec r100498.r_address <- c00425e4408000b4c3000000000000000000000000000000
--------------------
0x0: rol byte ptr [s5], 0xb4
--------------------
[100507] :: mov s2, &s5
[100509] :: add s7, s7, s2
[100512] :: mov s2, &flag[19]
[100514] :: mov(1) s5, s2
[100515] :: exec r100515.r_address <- c02c25e440800003c3000000000000000000000000000000
--------------------
0x0: shr byte ptr [s5], 3
--------------------
[100524] :: mov s2, &s5
[100526] :: add s7, s7, s2
[100529] :: mov s2, &flag[20]
[100531] :: mov(1) s5, s2
[100532] :: exec r100532.r_address <- c00c25e440800064c3000000000000000000000000000000
--------------------
0x0: ror byte ptr [s5], 0x64
--------------------
[100541] :: mov s2, &s5
[100543] :: add s7, s7, s2
[100546] :: madd s7 += (&flag[21] * 167)
[100604] :: mov s2, &flag[22]
[100606] :: mov(1) s5, s2
[100607] :: exec r100607.r_address <- c00425e440800051c3000000000000000000000000000000
--------------------
0x0: rol byte ptr [s5], 0x51
--------------------
[100616] :: mov s2, &s5
11. Aop
So this shellcode is just being used a mechanism to do more types of operations.
For example:
[100512] :: mov s2, &flag[19]
[100514] :: mov(1) s5, s2
[100515] :: exec r100515.r_address <- c02c25e440800003c3000000000000000000000000000000
--------------------
0x0: shr byte ptr [s5], 3
--------------------
[100524] :: mov s2, &s5
[100526] :: add s7, s7, s2
This block is computing s7 += (flag[19] >> 3).
We can define a new operation aop (add operation) that is similar to madd but also contains an operation specifier:
Aop = namedtuple('aop', ['dst', 'op', 'val', 'k', 'ridx'])
def lift_aop(instructions):
idx = 0
while idx < len(instructions):
match instructions[idx:idx+5]:
case [
Mov(Symbol(2), val, _, ridx),
Mov(Symbol(5), Symbol(2), _, _),
Shellcode(_, data, _),
Mov(Symbol(2), Ref(Symbol(5)), _, _),
Add(dst, dst2, Symbol(2), _)
] if len(data) == 24 and (dst == dst2):
op = next(md.disasm(data, 0))
t = op.mnemonic
k = int(op.op_str.split(', ')[-1], 16)
instructions[idx:idx+5] = [
Aop(dst, t, val, k, ridx)
]
idx += 1
return instructions
Sample 11 (1467 instructions)
// out madd computation
[64607] :: mov s5, &0
[64608] :: mov s7, &-393039
[64609] :: madd s7 += (&out[0] * 155)
[64667] :: madd s7 += (&out[1] * 190)
[64730] :: madd s7 += (&out[2] * 208)
[64778] :: madd s7 += (&out[3] * 123)
[64838] :: madd s7 += (&out[4] * 214)
[64896] :: madd s7 += (&out[5] * 146)
[64944] :: madd s7 += (&out[6] * 211)
[65002] :: madd s7 += (&out[7] * 85)
[65052] :: madd s7 += (&out[8] * 87)
[65107] :: madd s7 += (&out[9] * 251)
[65175] :: madd s7 += (&out[10] * 122)
[65230] :: madd s7 += (&out[11] * 60)
[65277] :: madd s7 += (&out[12] * 237)
[65340] :: madd s7 += (&out[13] * 27)
[65384] :: madd s7 += (&out[14] * 63)
[65441] :: madd s7 += (&out[15] * 207)
[65504] :: madd s7 += (&out[16] * 33)
[65541] :: madd s7 += (&out[17] * 138)
[65589] :: madd s7 += (&out[18] * 51)
[65636] :: madd s7 += (&out[19] * 103)
[65691] :: madd s7 += (&out[20] * 58)
[65738] :: madd s7 += (&out[21] * 68)
[65778] :: madd s7 += (&out[22] * 120)
[65828] :: madd s7 += (&out[23] * 111)
[65888] :: trunc s7 &= 0xffffff
[65891] :: mov s2, &s7
[65893] :: add s4, s4, s2
// flag 16-27 computation
[98563] :: mov s2, &s7
[98565] :: add s4, s4, s2
[98568] :: mov s7, &-62593
[98569] :: madd s7 += (&flag[16] * 162)
[98617] :: aop s7 += (&flag[17] ror 59)
[98634] :: madd s7 += (&flag[18] * 4)
[98657] :: aop s7 += (&flag[19] shl 0)
[98674] :: madd s7 += (&flag[20] * 207)
[98737] :: madd s7 += (&flag[21] * 128)
[98775] :: aop s7 += (&flag[22] ror 21)
[98792] :: aop s7 += (&flag[23] or 72)
[98809] :: madd s7 += (&flag[24] * 23)
[98853] :: aop s7 += (&flag[25] rol 1)
[98870] :: madd s7 += (&flag[26] * 247)
[98938] :: aop s7 += (&flag[27] shr 3)
[98955] :: trunc s7 &= 0xffffff
[98958] :: mov s2, &s7
[98960] :: add s4, s4, s2
[98963] :: mov s7, &-80711
[98964] :: madd s7 += (&flag[16] * 62)
[99016] :: aop s7 += (&flag[17] or 139)
[99033] :: madd s7 += (&flag[18] * 21)
[99072] :: madd s7 += (&flag[19] * 239)
[99140] :: madd s7 += (&flag[20] * 145)
[99188] :: madd s7 += (&flag[21] * 103)
[99243] :: aop s7 += (&flag[22] shr 0)
[99260] :: aop s7 += (&flag[23] rol 228)
[99277] :: madd s7 += (&flag[24] * 184)
[99330] :: madd s7 += (&flag[25] * 241)
[99388] :: madd s7 += (&flag[26] * 72)
[99428] :: aop s7 += (&flag[27] xor 38)
[99445] :: trunc s7 &= 0xffffff
[99448] :: mov s2, &s7
[99450] :: add s4, s4, s2
[99453] :: mov s7, &-98024
Part 3: Solution
Based on the previous disassembly, we can see that the constraint checker is dividied into chunks like this:
[98963] :: mov s7, &-80711
[98964] :: madd s7 += (&flag[16] * 62)
[99016] :: aop s7 += (&flag[17] or 139)
[99033] :: madd s7 += (&flag[18] * 21)
[99072] :: madd s7 += (&flag[19] * 239)
[99140] :: madd s7 += (&flag[20] * 145)
[99188] :: madd s7 += (&flag[21] * 103)
[99243] :: aop s7 += (&flag[22] shr 0)
[99260] :: aop s7 += (&flag[23] rol 228)
[99277] :: madd s7 += (&flag[24] * 184)
[99330] :: madd s7 += (&flag[25] * 241)
[99388] :: madd s7 += (&flag[26] * 72)
[99428] :: aop s7 += (&flag[27] xor 38)
[99445] :: trunc s7 &= 0xffffff
[99448] :: mov s2, &s7
[99450] :: add s4, s4, s2
Looking near the end, we see:
[101625] :: mov fail(), &0
[101626] :: exec s4 <- 8b0425cc408000f7d819c0c3000000000000000000000000
--------------------
0x0: mov eax, dword ptr [s4]
0x7: neg eax
0x9: sbb eax, eax
--------------------
[101635] :: mov s2, &s4
[101637] :: mov fail(), s2
So it looks like s4 must remain zero or else we will set the fail symbol and the flag will be invalid.
So our block above represents a summation of flag bytes operated on with another value. The summation plus -80711 (initial value of s7) must equal zero.
1. Flag pt.2
Similar to our lifters before, we can write a new function that patter matches on constraints with the second half of the flag (flag indexes 16 to 27) and pulls the expression into z3:
from z3 import *
def solve_end_flag(instructions):
orig = [BitVec('f%d' % i, 8) for i in range(16,28)]
flag = ([0] * 16) + [ZeroExt(24, x) for x in orig]
s = Solver()
for o in orig:
s.add(UGT(o, 0x20))
s.add(ULT(o, 0x7f))
idx = 0
while idx < len(instructions):
match instructions[idx]:
case Mov(Symbol(7), Ref(v), _, ridx) if type(v) is int:
x = BitVecVal(v, 32)
ptr = idx+1
while ptr < len(instructions):
match instructions[ptr]:
case MultAdd(Symbol(7), Ref(FlagAddr(f)), k, _):
x += (flag[f] * k)
case Aop(Symbol(7), op, Ref(FlagAddr(f)), k, _):
v = None
match op:
case 'and': v = flag[f] & k
case 'xor': v = flag[f] ^ k
case 'or': v = flag[f] | k
case 'rol': v = ZeroExt(24, RotateLeft(Extract(7,0,flag[f]), k))
case 'ror': v = ZeroExt(24, RotateRight(Extract(7,0,flag[f]), k))
case 'shl': v = ZeroExt(24, Extract(7,0,flag[f]) << k)
case 'shr': v = flag[f] >> k
case _:
raise Exception(f'unknown aop: {op}')
x += v
case Trunc(Symbol(7), k, _):
s.add(x == 0)
case _:
break
ptr += 1
idx += 1
print(s.check())
m = s.model()
flag = bytes([m.eval(o).as_long() for o in orig])
return flag
We get:
sat
b'3_3LF_m4g1c}'
2. Output array
I tried doing the same z3 solution for the out array checks (which just use madd) but it was taking a while to solve. ahem
ctf players would rather solve a linear system in z3 than learn what a matrix is
— cts (@gf_256) July 2, 2022
Each individual constraint with only madd is equivalent to one row of a matrix multiplication and since there are exactly 24 out values and 24 constraints, we can solve this matrix.
Instead of using z3, we can pull out the actual matrix and use np.linalg.solve to solve it:
import numpy as np
# ---
def solve_out_arr(instructions):
X = []
Y = []
idx = 0
while idx < len(instructions):
match instructions[idx]:
case Mov(Symbol(7), Ref(v), _, ridx) if type(v) is int:
row = []
ptr = idx+1
while ptr < len(instructions):
match instructions[ptr]:
case MultAdd(Symbol(7), Ref(OutAddr(_)), k, _):
row.append(k)
case Trunc(Symbol(7), k, _):
X.append(row)
Y.append(-v)
case _:
break
ptr += 1
idx += 1
a = np.array(X, dtype=np.uint32)
b = np.array(Y, dtype=np.uint32)
return [int(x) for x in np.linalg.solve(a,b)]
We get:
[134, 72, 7, 236, 29, 49, 88, 228, 231, 231, 227, 16, 242, 80, 242, 1, 224, 113, 46, 224, 108, 91, 103, 182]
3. Flag pt.1
This out array was computed based on the first 16 bytes of the flag with these blocks:
[0347] :: shuffleblock &flag[0], &flag[1]
[8028] :: mov s4, &0
[8029] :: output out[0], &arr[0]
[8071] :: output out[1], &arr[1]
[8113] :: output out[2], &arr[2]
[8155] :: reset
[8411] :: mov s4, &0
[8412] :: shuffleblock &flag[2], &flag[3]
[16092] :: mov s4, &0
[16093] :: output out[3], &arr[0]
[16135] :: output out[4], &arr[1]
[16177] :: output out[5], &arr[2]
[16219] :: reset
[16475] :: mov s4, &0
[16476] :: shuffleblock &flag[4], &flag[5]
[24156] :: mov s4, &0
[24157] :: output out[6], &arr[0]
[24199] :: output out[7], &arr[1]
[24241] :: output out[8], &arr[2]
[24283] :: reset
Specifically, out[0:3] is derived from flag[0:2]. out[3:6] is derived from flag[2:4], etc…
We can simply brute force each pair of flag bytes to solve for a given output triplet:
def solve_start_flag(output):
def sim(a,b):
arr = list(range(256))
z = 0
for i in range(256):
p = a if i % 2 == 0 else b
z = (z + arr[i] + p) & 0xff
arr[i], arr[z] = arr[z], arr[i]
out = [0,0,0]
z = 0
for i in range(3):
z = (z + arr[i]) & 0xff
arr[i], arr[z] = arr[z], arr[i]
out[i] = arr[(arr[i] + arr[z]) & 0xff]
return out
def solve_chunk(k1,k2,k3):
# Brute force chunk.
for a in range(0x20, 0x7f):
for b in range(0x20, 0x7f):
out = sim(a,b)
if abs(out[0] - k1) <= 1 and abs(out[1] - k2) <= 1 and abs(out[2] - k3) <= 1:
return (a,b)
return None
f = []
for i in range(0,len(output),3):
f += list(solve_chunk(*output[i:i+3]))
return bytes(f)
This gives us:
CTF{H0p3_y0u_l1k
Our final flag is: CTF{H0p3_y0u_l1k3_3LF_m4g1c}
Conclusion
See the full solve script here: https://gist.github.com/hgarrereyn/9e536e8b3471d3cb8ecbb5932a776b95
I really enjoyed this challenge; weird VM reversing is one of my favorite subcategories and this one proved to be especially tricky due to self modifying code.