justCTF 2019 - Walking Simulator (474pt)
reversing
December 22, 2019
reversing
black box
Walking Simulator (474pt)
Reversing
Description: You have given a three graphs. And three final permutations of partial flag permutations. (A i-th perm is modified by a i-th binary) Can you retrieve the flag?
TLDR: black box the fuck out of it
Overview:
We are given three binaries: part_1, part_2 and part_3 and a python script: public.py.
Essentially, you run public.py with a flag and it is chunked into 16-byte blocks each of which are turned into a permutation of 37 numbers, for example:
36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 4 6 0 1 3 2 5
When you run the binary, you provide this initial permutation and then need to make choices:
$ ./part_1
FLAG PERMUTATION: 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 4 6 0 1 3 2 5
Ok, let's start!
Starting a step.
You are in middle node.
Choice:
4
terminate called after throwing an instance of 'std::invalid_argument'
what(): Incorrect path!
Aborted
Most of the time, this will fail with the message like the one above. With some values however, you will get another prompt:
$ ./part_1
FLAG PERMUTATION: 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 4 6 0 1 3 2 5
Ok, let's start!
Starting a step.
You are in middle node.
Choice:
9
Starting a step.
You are in middle node.
Choice:
Finally, we are provided with three files: flag_perm_1.out, flag_perm_2.out, flag_perm_3.out:
flag_perm_1.out
Good job!
11 23 29 10 19 30 27 5 22 25 35 26 12 18 13 17 8 31 9 15 3 36 33 32 14 24 6 20 28 2 1 34 7 0 4 21 16
This file supposedly contains output from running part_1 on the first flag chunk.
So now we understand the dataflow is flag --> permuation --> new permuation.
We are provided with new permutation and we need to reverse the previous two steps to obtain the flag.
Part One: factoradic
I started with the initial python script first since python is generally more comfortable to reverse.
The script is below (restructured a bit and with some comments):
from functools import lru_cache
from Crypto.Util.number import bytes_to_long
@lru_cache(1024)
def factorial(n):
return 1 if n == 0 else n * factorial(n-1)
def int_to_perm(v):
assert v < factorial(PERM_SIZE)
tmp = []
for x in range(PERM_SIZE-1, -1, -1):
tmp += [ v // factorial(x) ]
v = v % factorial(x)
tmp = tmp[::-1]
ret = []
for i in range(PERM_SIZE):
p = tmp[i]
ret = ret[:p] + [i] + ret[p:]
return ' '.join(map(str, ret))
PERM_SIZE = 37
def flag_to_perms(flag):
assert len(flag) % 16 == 0, "Incorrect flag len"
# chunk flag into 16 byte parts
parts = [ flag[i*16:(i+1)*16].encode() for i in range(len(flag)//16) ]
# convert to integer
VALS = map(bytes_to_long, parts)
# generate permutations
return list(map(int_to_perm, VALS))
flag = input()
perms = flag_to_perms(flag)
print(*perms, sep='\n')
for i in range(len(flag)//16):
with open("flag_perm_" + str(i+1) + ".in", "w") as f:
f.write(perms[i])
Essentially, the script interprets each 16-byte chunk as an integer and calls int_to_perm.
The first loop looks similar to decoding a number in a specific base, except instead of dividing by base^i, we are dividing by factorial(i).
Interestingly, this is a valid number system: https://en.wikipedia.org/wiki/Factorial_number_system
The second loop constructs a permuation of range(37) using this representation.
However, since numbers are always added in order, the index of 36 tells us tmp[36] and after removing this number, the index of 35 tells us tmp[35] and so on…
I implemented this with the following function:
def perm_to_int(p):
# input is a string permutation: '36 35 34 ... 3 2 5'
ret = [int(x) for x in p.split(' ')]
tmp = []
for i in range(PERM_SIZE-1, -1, -1):
idx = ret.index(i)
tmp.append(idx)
ret = ret[:idx] + ret[idx+1:]
# tmp represents the integer in factoradic
tmp = tmp[::-1]
f = 0
for i in range(PERM_SIZE):
f += tmp[i] * factorial(i)
return f
Ok, so now we understand the first part of the dataflow and we need to reverse the binaries.
Part Two: The binaries
All three binaries are very similar with slightly different data.
When we open part_1, we are confronted with familiar c++ mangled function names.
Main looks like this:
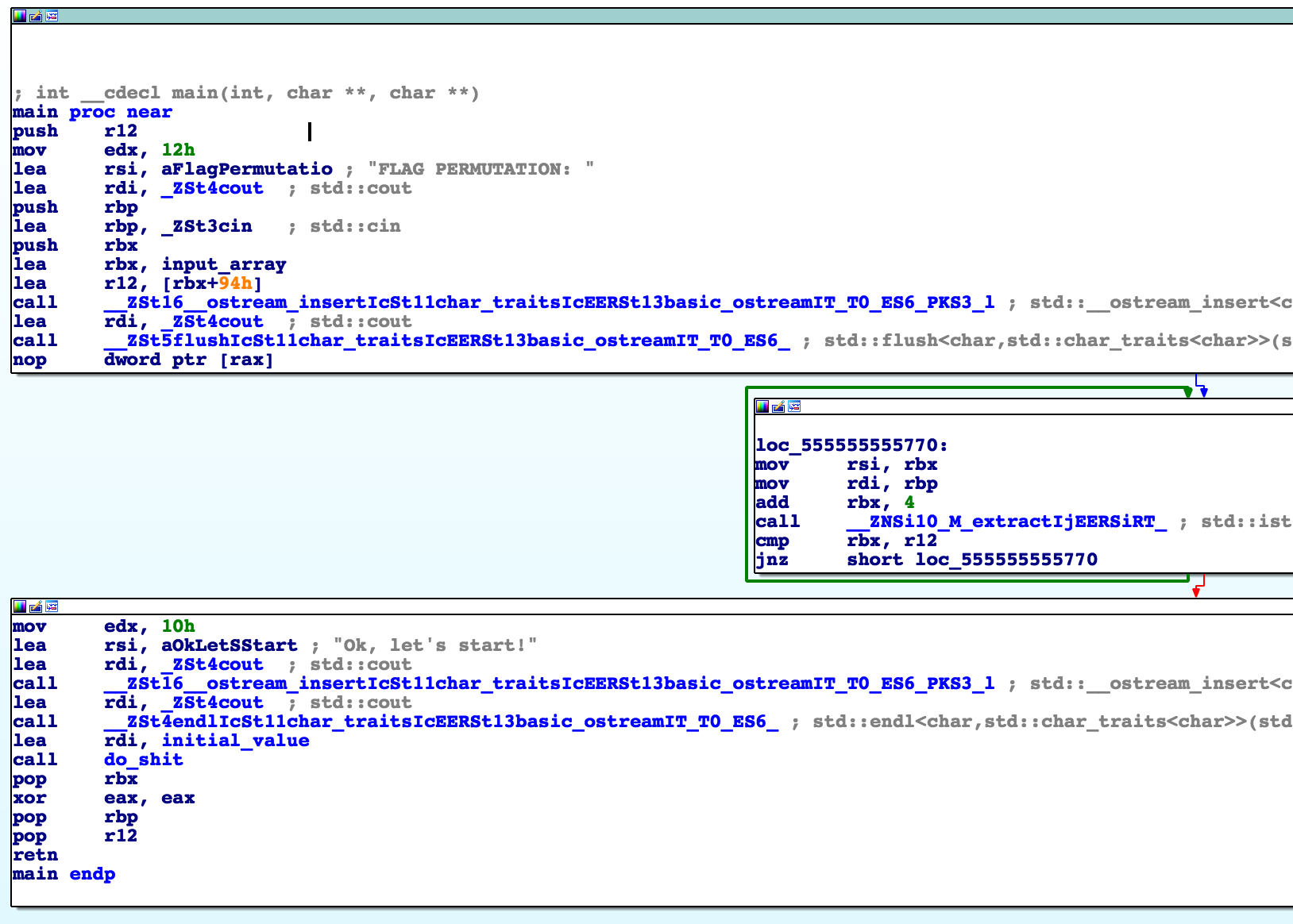
This code is responsible for printing FLAG PERMUTATION: and then reading the numbers into a global array.
Then it calls do_shit with a global paramater (in part_1 this is 0x23).
That function looks like:
I started looking into these functions and was confronted with an overwhelming amount of nested comparisons and nested function calls:
Whenever you see this, you know you’re in for a treat:
At this point it was clear that reversing the entire binary would be impossible within the time constraint. Instead we need to find a clever way to solve the challenge.
Recently with RE challenges, I’ve been using a technique where I write down clear questions about the program on paper and try to answer them. This helps me stay focused on one train of thought rather than getting lost jumping around the binary. It also helps ensure I’m always making forward progress and not just spinning my wheels.
I’ll try to replay my though process here:
1. What is the goal state?
This is always a good place to start for reversing challenges. We know that our output contains the string “Good job!” so let’s find it.
This string is referenced in a single function in the binary:
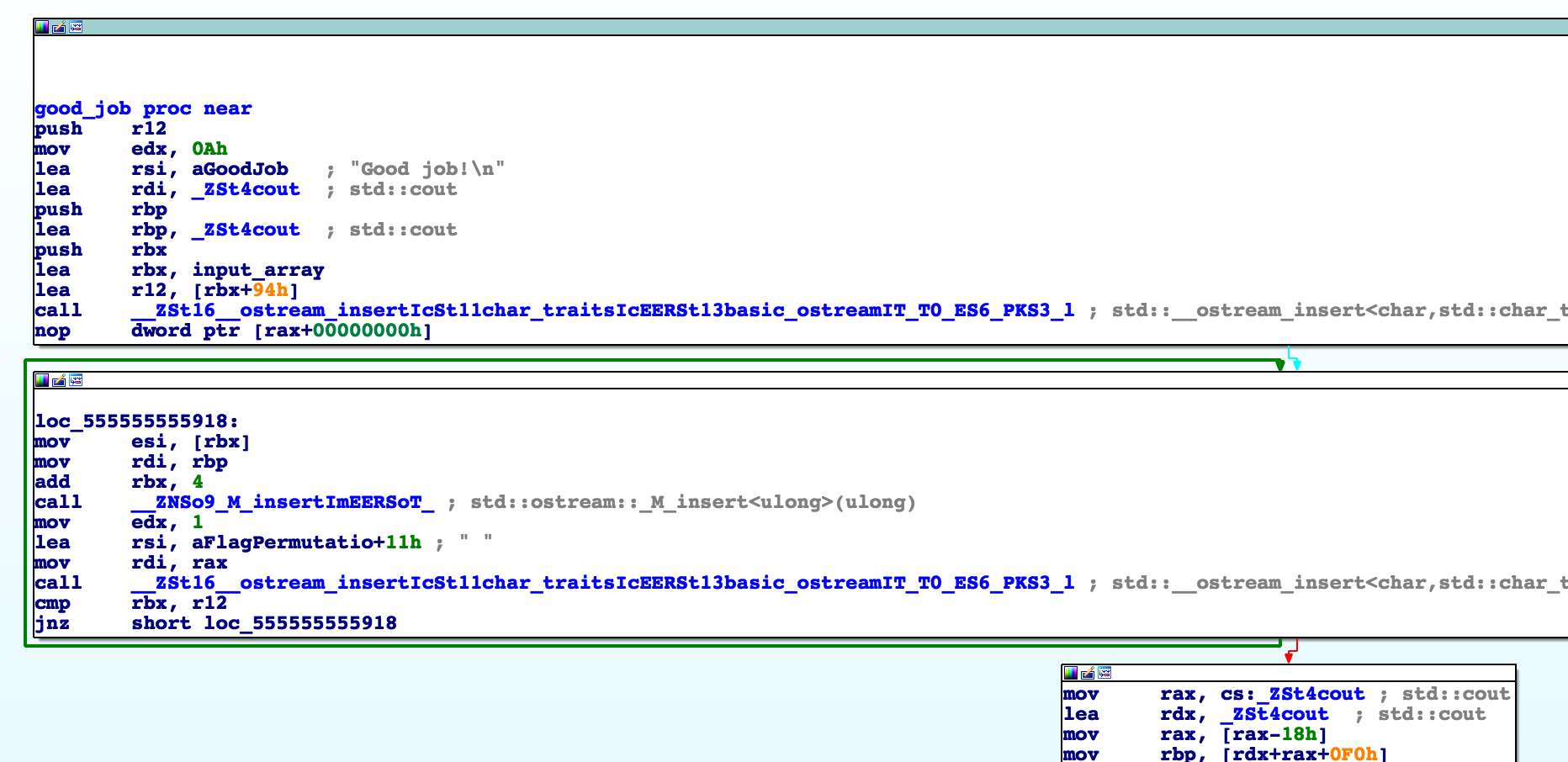
Here we also see code that prints out input_array which was where our original permutation was stored.
We can examine the cross references to this goal state and it is found only once here:

This function, respectively, is called here:
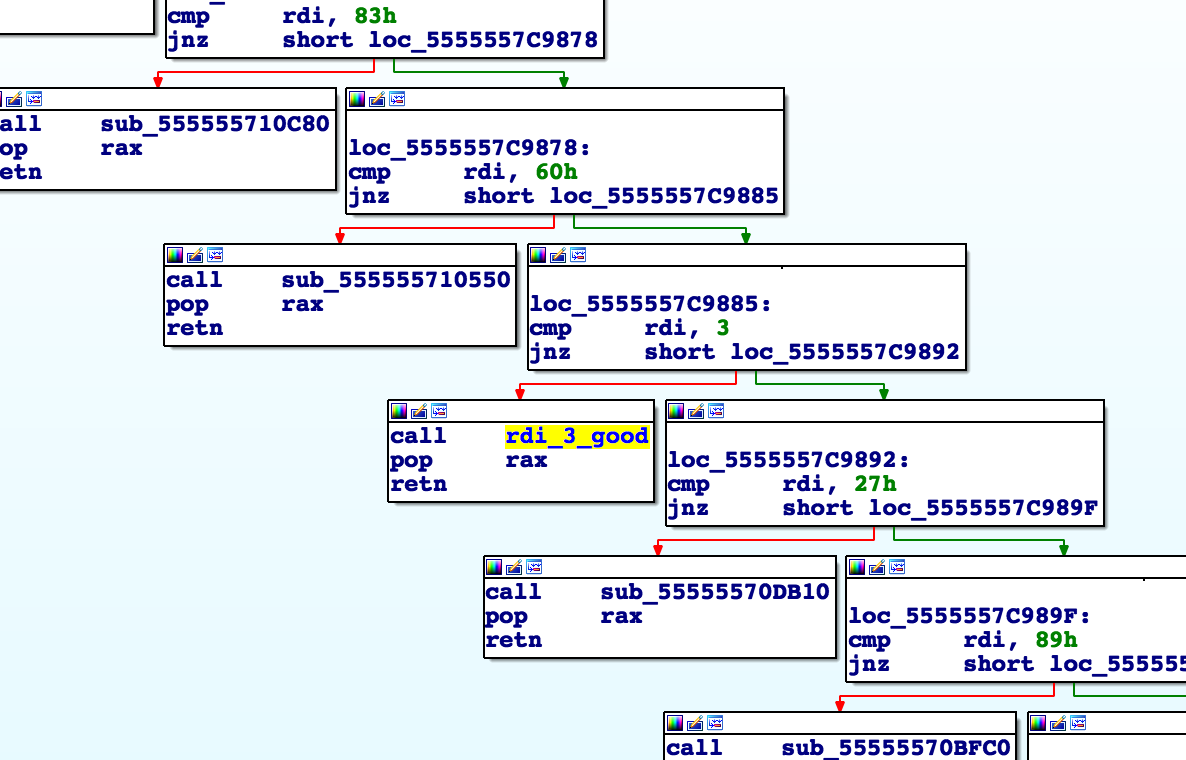
This function happens to be print_node_type_scramble from our original do_shit loop.
Additionally, here we see that rdi (the only input) must be 3.
2. Does our original input actually change or is this “choice” stuff just obfuscation?
Since the goal state prints from the same buffer as our original input, I was curious if it is ever modified.
I set a breakpoint right before the call to print_node_type_scramble and iterated choices until I found that 9 was valid.
After examining memory, our original permutation has been shuffled.
To test this, I wrote a python script that would bruteforce choices and I discovered that several choices were valid for the initial state such as: 9,13,23,30…
3. Do the valid choices depend on our input permutation?
With my bruteforcing script, I tested several input permutations and discovered that the set of valid choices was the same regardless of what input permutation you provided.
This simplifies our understanding of the binary since we know the “correct path” must be hardcoded into the binary in one form or another.
4. Do the valid choices depend on the history or just the current state?
In the do_shit loop, [rbp+0] acts as a state marker that updates at each loop.
I was curious if this was the only parameter to determine what choices were valid.
To test this, I used the fact that 9, 24 were two valid moves (found by bruteforcing).
Specifically, our initial state is 0x23 and 9 transitions us to 0x36.
In the initial state 24 throws an error and 9 is valid.
However, if we dynamically patch [rbp+0] to 0x36 in the first iteration, we would expect 24 to be a valid move and 9 to be invalid.
Luckily, this is the observed behavior.
Therefore, the binary behaves like a DFA where each state transition has the side effect of permuting the flag.
Our goal is to find a path from the start state (0x23) to the end state (0x3).
5. Can we dump the transition table?
Let’s go back to the main loop and anaylize it at a higher level with our new understanding:

It’s basically doing this:
state = 0x23
while True:
# print_node_type_scramble
if state == 0x3:
print('Good job!')
return
choice = int(raw_input())
next_state = get_new_val(fuck_me(state, choice))
# this might throw an error internally
if check_invalid_path(state, next_state):
state = next_state
else:
exit(-1)
I tried several different methods to interface these methods in a black-box format and eventually settled on using a python script communication to a gdb process.
In gdb you can define function pointers and then actually emulate function calls like:
pwndbg> set $fuck = (int (*)(int, int))0x555555556380
pwndbg> set $get_val = (int (*)(int))0x5555556EEB00
pwndbg> set $check = (int (*)(int, int))0x555555555C00
pwndbg> p $fuck(0x23, 0x9)
$1 = 158
pwndbg> p $get_val(158)
$2 = 54
pwndbg> p $check(0x23, 54)
$3 = 1
Using this technique I wrote a script to dump every (state, choice, next) tuple where the validation check $check(state, next) passes.
6. Final steps
With a transition table you can do a DFS from the end state and find a valid path.
Using the discovered sequence of choices, we can uncover the permutation mapping.
I opted to send a sequence of all 0’s and a single 1 in a specific spot.
Then by recording where the 1 ends up, you can decode the mapping.
Luckily for us, the final permutation mapping also doesn’t depend on the original input (which is something I didn’t explicitly test before this stage).
Now, using this mapping, it is simply a matter of reversing the flag output and decoding it as bytes.
The other two binaries were very similar and I just needed to adjust breakpoints and address locations to use the same solution scripts.