HackTM 2020 - mama bear (499pt)
jit reversing + z3
February 5, 2020
reversing
mama bear (499pt)
Reversing
Description: Author: trupples
Despite Goldilocks' bad encounters with the bear family, mama bear seems to like her, and they’ve been talking using cryptography. Papa bear remembers hearing her say: “Haha more like 8ba409960881fbab676e7e4a47447770b365d57c186169286b2f064d0b434bf6”
Can you find out what she actually told Goldilocks?
P.S. to make your search easier, baby bear has noticed Goldilocks always starts her passwords with a capital X and ends them with a capital W.
Files:
Overview:
We are given an ELF mama_bear that takes an 8-byte password and a 32-byte “secret” and spits out a new 32-byte message:

Our goal is to find the correct password and secret so that we see the output: 8ba409960881fbab676e7e4a47447770b365d57c186169286b2f064d0b434bf6
Reversing:
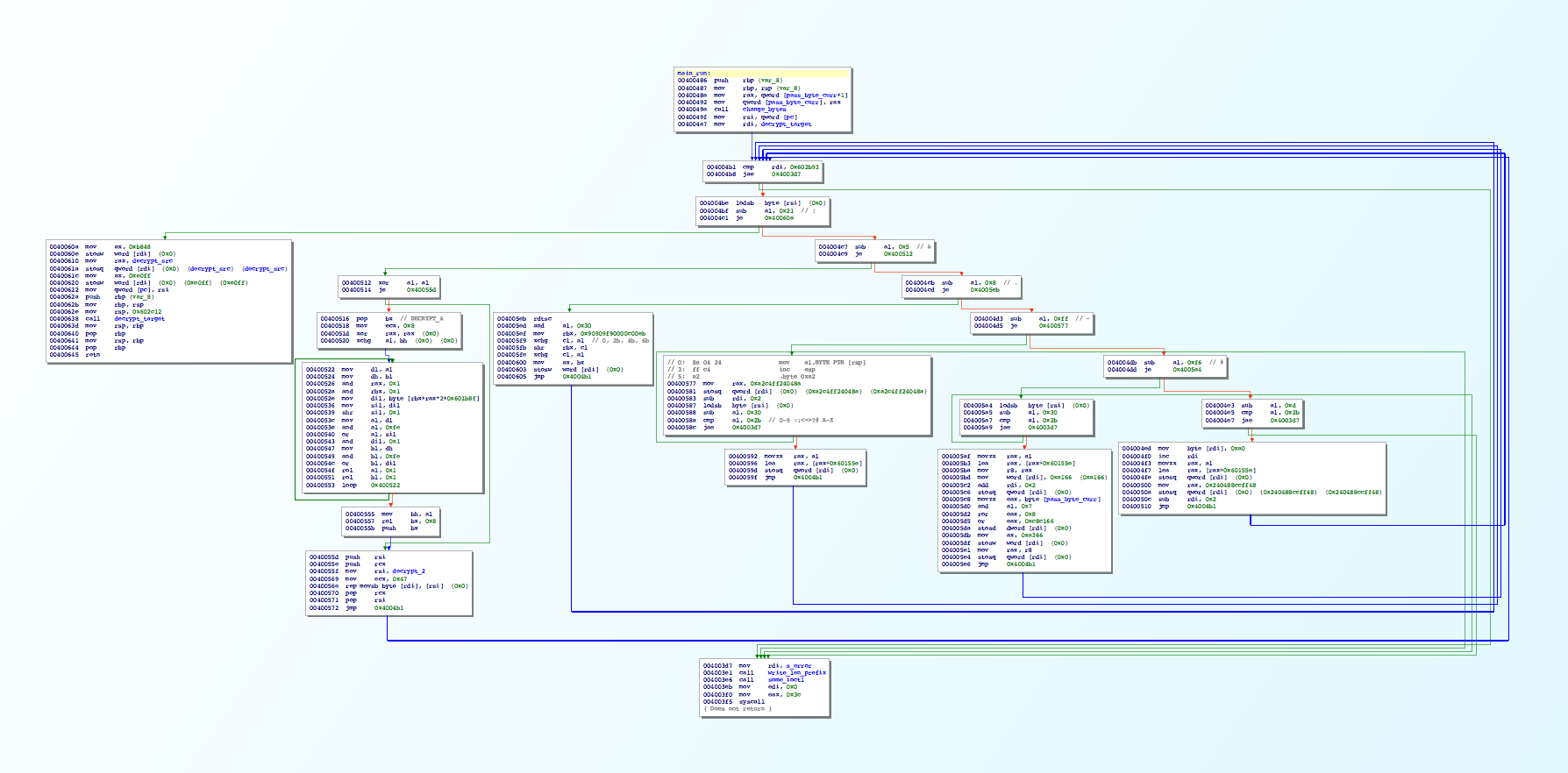
The program is pretty small and our _start function consists of some string printing calls, a call to read user input and several calls to this function:
Additionally, we find this following suspicious data in memory:
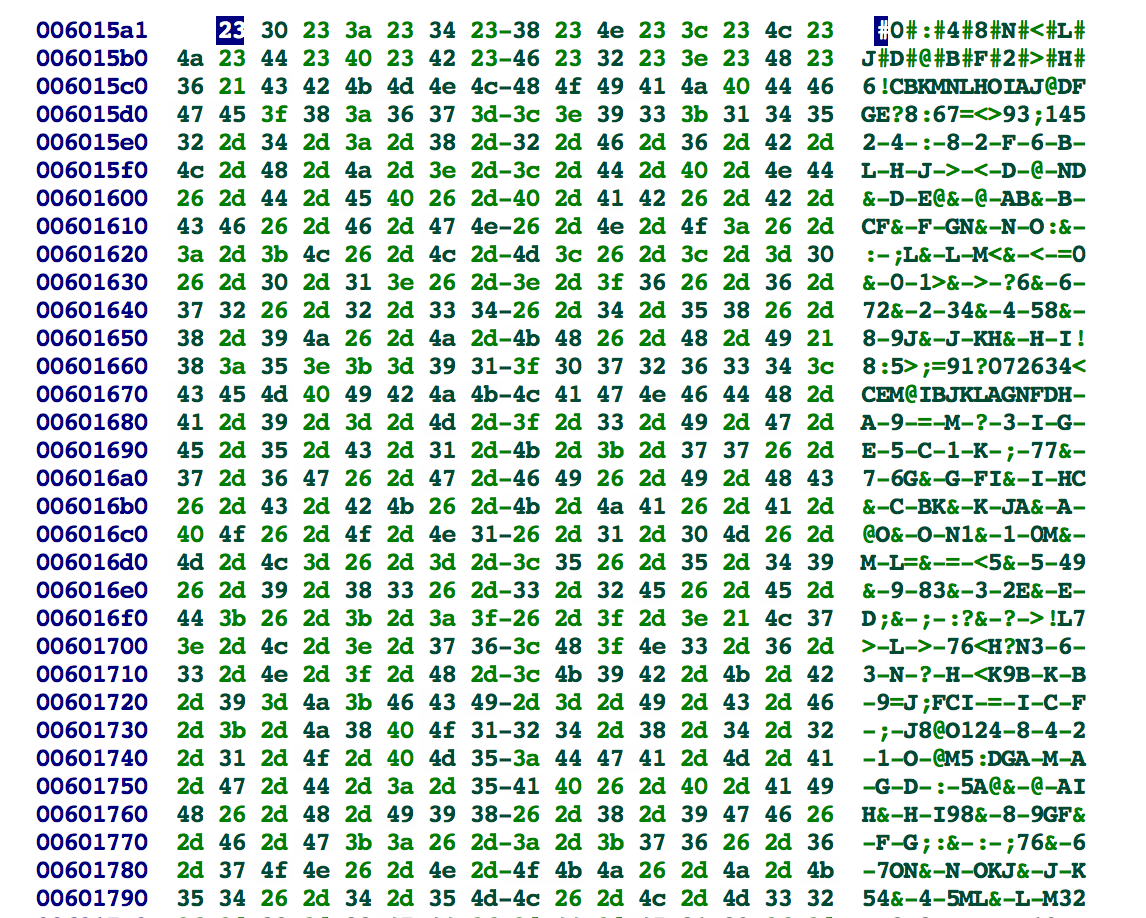
This pattern of a switch statement inside a loop usually indicates some sort of virtual machine. The suspicious memory string is likely our encoded program.
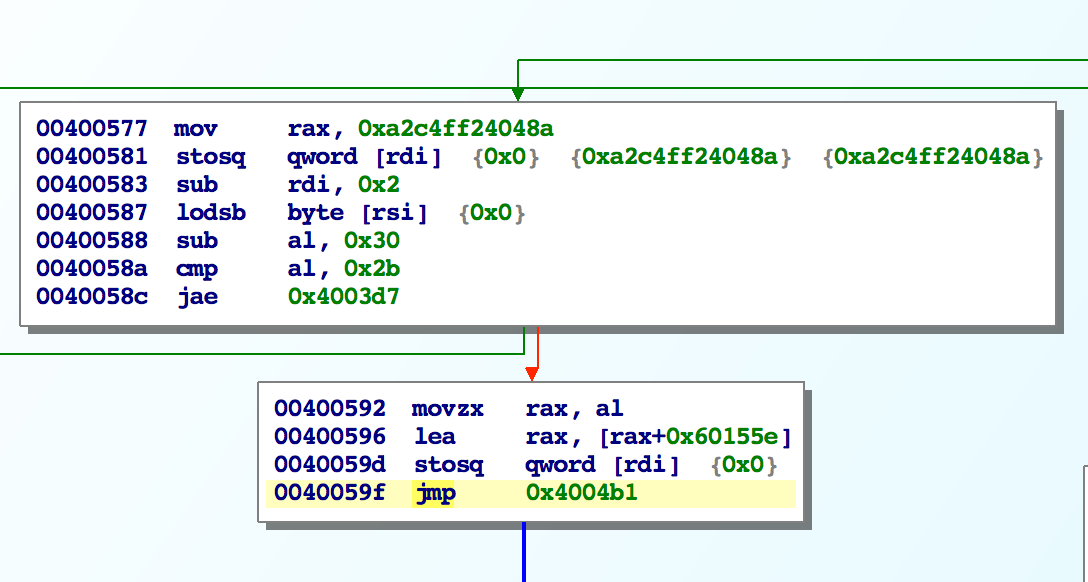
After some reversing, we see that rsi is acting as our program counter in this function. However the opcode cases look strange: there are weird constants and it’s hard to understand what the function is. For example here is the case for the - opcode:
So we are writing some strange constant to [rdi] loading another byte from rsi and writing more data to rdi. We can also see that at the start of this function, rdi is set to the address of a subroutine:
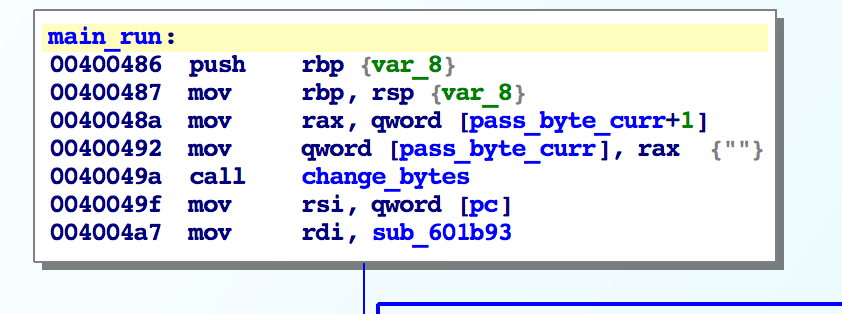
Hmmm… so maybe we should interpret these constants as machine code…
When we do that it makes a lot more sense. For the - opcode, we have the pattern:
0: 8a 04 24 mov al,BYTE PTR [rsp]
3: ff c4 inc esp
5: a2 5e 15 60 00 00 00 movabs ds:0x60155e+<x>,al
where <x> is the value encoded in the second byte of the opcode (ascii value minus 0x30).
So this opcode is pushing x86 instructions that implement a POP operation. Specifically, we are using the native stack pointer (rsp) and it looks like 0x60155e is some sort of memory buffer.
As a whole, this function is implementing a sort of JIT-compilation step to translate the program into x86. The final opcode ! adds the function prologue and executes the instruction.
Following this same pattern we can decode all the operations:
#<x> :: M[x:x+2] >>= (pass & 7) :: rotate two bytes at a
:: time by the current pass byte
<x> :: PUSH M[x] :: push M[x] to the stack
-<x> :: POP M[x] :: pop into M[x]
& :: MUT :: pop the top two values,
:: mutate them with a crypto
:: func and push them back
! :: EXEC :: execute the JIT function
<x> is an integer in the range [0,0x2d) that is encoded by the ascii value x + 0x30.
After some more reversing we see that this VM function is called 9 times, the first time is actually before we enter any input and we see that the memory buffer is set to: https://twitter.com/_trupples <3
Then the vm function is called 8 more times (on 8 subsequent program strings) and each time the next byte of our password input is set in a global variable which influences the operation of the MUT and ROTATE operations (& and #).
Solution:
To solve this problem, I implemented the program execution in z3 at a relatively high level and symbolically solved for the original password and secret.
If you are not familiar, z3 is a constraint solver that allows you to define a set of constraints and obtain a solution. Basically it’s black magic and it comes in very handy for certain types of reversing problems.
I’ll walk through my solution script in this section:
We start with the import:
from z3 import *
Now we can initialize a Solver and create the symbolic variables to hold our initial password and secret:
# init solver
s = Solver()
# add password
password = [BitVec('p%d' % i, 8) for i in range(8)]
# known bytes
s.add(password[0] == ord('X'))
s.add(password[7] == ord('W'))
# add mem
mem = [BitVec('m%d' % i, 8) for i in range(32)]
# keep a reference to the original memory (as we will modify the list above)
orig_mem = [k for k in mem]
Next we can constrain the bytes of the password we know (from the description) and constrain both values to ascii:
# known bytes
s.add(password[0] == ord('X'))
s.add(password[7] == ord('W'))
# constrain password and secret to ascii
for o in orig_mem:
s.add(And(ULE(o,0x7f), o>0x1f))
for p in password:
s.add(And(ULE(p, 0x7f), p>0x1f))
During the MUT function, we have a relatively complex operation that pops two bytes from the stack, does some bit manipulation and pushes them back:
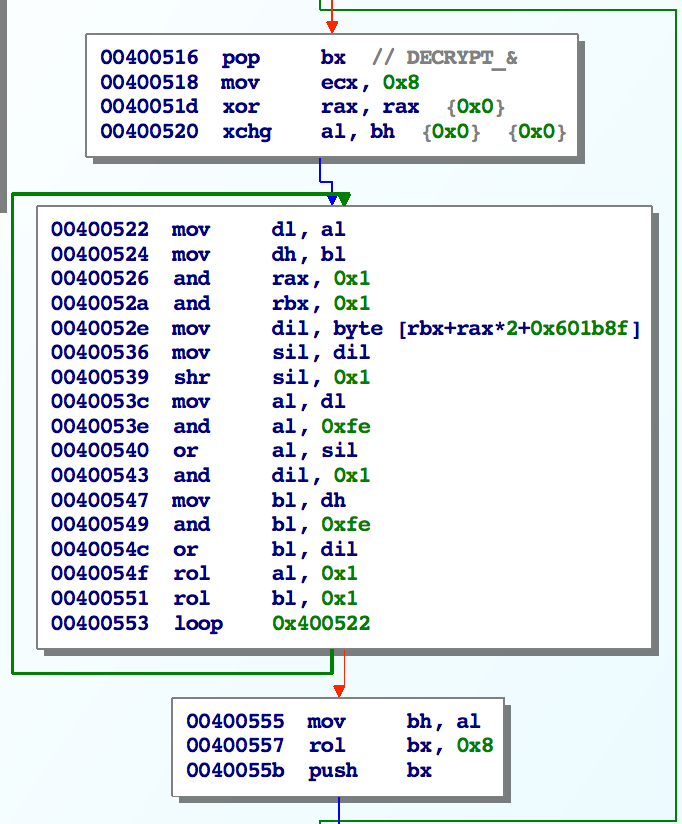
Rather than try to figure out what this does at a high level, I just implemented the x86 instructions directly in z3. The address at 0x601b8f points to a 4 element array that is computed as a function of the current password character. Since there are only 256 values, I decided to just dump all the possible lookup arrays and index by the current password byte. Using a simple gdb script, I dumped all the possible values:
# dumped with gdb script
BOX = [[1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2], [1, 3, 0, 2], [2, 3, 0, 1], [3, 2, 0, 1], [0, 2, 3, 1], [1, 0, 3, 2], [2, 0, 3, 1], [3, 0, 2, 1], [0, 3, 2, 1], [1, 2, 3, 0], [2, 1, 3, 0], [3, 1, 2, 0], [0, 1, 2, 3], [1, 3, 2, 0], [2, 3, 1, 0], [3, 2, 1, 0], [0, 2, 1, 3], [1, 0, 2, 3], [2, 0, 1, 3], [3, 0, 1, 2], [0, 3, 1, 2], [1, 2, 0, 3], [2, 1, 0, 3], [3, 1, 0, 2], [0, 1, 3, 2]]
Originally I stored these values in a 1024 element matrix (256 * 2 * 2) and indexed by the current password byte and the two computed bits. However, I found it was more performant to use a 256 element array indexed by the password byte and pack the 4 2-bit values into a single 8-bit BitVec:
# concatenate to improve z3 performance
BOX_CONCAT = []
for b in BOX:
v = b[0] + (b[1]<<2) + (b[2]<<4) + (b[3]<<6)
BOX_CONCAT.append(v)
In order to use these result of an indexing operation in a z3 expression, we need to make this array symbolic:
# add the array
S_BOX_CONCAT = Array('box', BitVecSort(8), BitVecSort(8))
for j in range(len(BOX_CONCAT)):
s.add(S_BOX_CONCAT[j] == BOX_CONCAT[j])
Essentially, we are initializing a symbolic array that maps an 8-bit BitVec to an 8-bit BitVec. Then we are constraining the values of this array to specific (pre-computed) static values.
Now we can implement the MUT function as follows:
# simulate this at a really low level so I don't fuck it up
def mut(pass_byte, a, b, box):
bl = a
bh = b
al,bh = bh,bl
for i in range(8):
# print(hex(al),hex(bl))
dl = al
dh = bl
al &= 1
bl &= 1
dil = LShR(LShR(box[pass_byte], al*4), bl*2) & 3
sil = LShR(dil, 1)
al = dl
al &= 0xfe
al |= sil
dil &= 1
bl = dh
bl &= 0xfe
bl |= dil
al = ((al << 1) | LShR(al, 7)) & 0xff
bl = ((bl << 1) | LShR(bl, 7)) & 0xff
bh = al
bl,bh = bh,bl
return (bl, bh)
Next we define the function strings (obtained from program memory):
# functions
f1 = 'CBKMNLHOIAJ@DFGE?8:67=<>93;1452-4-:-8-2-F-6-B-L-H-J->-<-D-@-ND&-D-E@&-@-AB&-B-CF&-F-GN&-N-O:&-:-;L&-L-M<&-<-=0&-0-1>&->-?6&-6-72&-2-34&-4-58&-8-9J&-J-KH&-H-I'
f2 = '8:5>;=91?072634<CEM@IBJKLAGNFDH-A-9-=-M-?-3-I-G-E-5-C-1-K-;-77&-7-6G&-G-FI&-I-HC&-C-BK&-K-JA&-A-@O&-O-N1&-1-0M&-M-L=&-=-<5&-5-49&-9-83&-3-2E&-E-D;&-;-:?&-?->'
f3 = 'L7>-L->-76<H?N3-6-3-N-?-H-<K9B-K-B-9=J;FCI-=-I-C-F-;-J8@O124-8-4-2-1-O-@M5:DGA-M-A-G-D-:-5A@&-@-AIH&-H-I98&-8-9GF&-F-G;:&-:-;76&-6-7ON&-N-OKJ&-J-K54&-4-5ML&-L-M32&-2-3ED&-D-E10&-0-1?>&->-?=<&-<-=CB&-B-C'
f4 = 'C7@1LI-C-I-L-1-@-74F=-4-=-FKG?0NM-K-M-N-0-?-GHA3-H-3-A5D9<6B-5-B-6-<-9-DJE;8>2-J-2->-8-;-EFG&-G-FNO&-O-NBC&-C-BDE&-E-D@A&-A-@67&-7-689&-9-8<=&-=-<JK&-K-J01&-1-0HI&-I-H45&-5-423&-3-2LM&-M-L>?&-?->:;&-;-:'
f5 = 'JKFEH@IMCGANLDOB<9;5>728:=463?1-2-N-6-<-8-J-D-@-4->-L-:-F-B-HJ&-J-K0&-0-1F&-F-G6&-6-72&-2-3L&-L-M@&-@-AH&-H-I4&-4-5<&-<-=N&-N-O>&->-?D&-D-EB&-B-C8&-8-9:&-:-;'
f6 = '862:>1?3;=<47950JMFHENDC@ILABKG-?-G-5-3-I-C-1-7-9-M-;-A-=-K-EO&-O-NE&-E-D=&-=-<A&-A-@G&-G-F7&-7-65&-5-49&-9-8I&-I-H1&-1-0M&-M-L3&-3-2;&-;-:K&-K-JC&-C-B?&-?->'
f7 = 'L7>-L->-7I=J;FC-I-C-F-;-J-=9BK-9-K-B5:DGAM-5-M-A-G-D-:1248@O-1-O-@-8-4-236<H?N-3-N-?-H-<-610&-0-154&-4-5?>&->-?ON&-N-OGF&-F-GA@&-@-A32&-2-3ED&-D-E;:&-:-;CB&-B-CIH&-H-IKJ&-J-KML&-L-M=<&-<-=98&-8-976&-6-7'
f8 = '<6B5D9-<-9-D-5-B-6HA3-H-3-A4F=-4-=-F7@1LIC-7-C-I-L-1-@G?0NMK-G-K-M-N-0-?>2JE;8->-8-;-E-J-2HI&-I-HJK&-K-J01&-1-0<=&-=-<LM&-M-LFG&-G-F67&-7-645&-5-4@A&-A-@>?&-?->89&-9-8DE&-E-DBC&-C-BNO&-O-N23&-3-2:;&-;-:' # #2#B#F#4#0#8#>#D#@#H#L#N#:#J#6#<'
# (last one is truncated to remove rotation instructions)
Finally we are ready to symbolically execute the functions:
# symbolically execute a program
def process_func(prog, mem, pass_byte, box):
STACK = [None] * 32
stack_i = 0
pc = 0
while pc < len(prog):
curr = prog[pc]
pc += 1
if curr == '#':
# rotate
x = ord(prog[pc]) - 0x30
pc += 1
ror = (pass_byte & 0x7)
val = Concat(mem[x+1], mem[x])
val = RotateRight(val, ror)
mem[x+1] = Extract(15,8,val)
mem[x] = Extract(7,0,val)
elif curr == '-':
# pop
x = ord(prog[pc]) - 0x30
pc += 1
stack_i -= 1
mem[x] = STACK[stack_i]
elif curr == '&':
# mut
t0 = STACK[stack_i-1]
t1 = STACK[stack_i-2]
x,y = mut(pass_byte,t0,t1,box)
STACK[stack_i-1] = x
STACK[stack_i-2] = y
else:
# push
x = ord(curr) - 0x30
STACK[stack_i] = mem[x]
stack_i += 1
This function takes a program string, memory array, current password byte and the lookup table we created earlier. Stack manipulation is done by moving pointers between the STACK list and the mem list. When we compute mut for example, it returns two symbolic expressions that are stored back on the stack.
Now we can use this in our original program:
# symbolically execute the functions
process_func(f1, mem, password[0], S_BOX_CONCAT)
process_func(f2, mem, password[1], S_BOX_CONCAT)
process_func(f3, mem, password[2], S_BOX_CONCAT)
process_func(f4, mem, password[3], S_BOX_CONCAT)
process_func(f5, mem, password[4], S_BOX_CONCAT)
process_func(f6, mem, password[5], S_BOX_CONCAT)
process_func(f7, mem, password[6], S_BOX_CONCAT)
process_func(f8, mem, password[7], S_BOX_CONCAT)
Finally, we tell z3 what the target output should be and also constrain a few bytes of the input to conform to flag format:
# (this is the target pre-rotation)
target = 'd2 45 cb 04 40 84 d5 fd b7 33 25 3f a2 23 b8 3b b2 d9 be 6a 30 8c 94 34 97 b5 26 83 a1 85 fb 25'
target = [int(x,16) for x in target.split(' ')]
# constrain mutated secret to the target
for i in range(len(target)):
s.add(mem[i] == target[i])
# constrain original secret to flag format
s.add(orig_mem[0] == ord('H'))
s.add(orig_mem[1] == ord('a'))
s.add(orig_mem[2] == ord('c'))
s.add(orig_mem[3] == ord('k'))
Now all we need to do is let it run:
# may take a few minutes
s.check()
# print flag
m = s.model()
print(''.join([chr(m[x].as_long()) for x in orig_mem]))
HackTM{By3_bYE_G0Ld!l0cKS_~mama}
For a full solution script see here